Punkty \(A, B, C\) leżą na okręgu o środku \(S\). Punkt \(D\) jest punktem przecięcia cięciwy \(AC\) i średnicy okręgu poprowadzonej z punktu \(B\). Miara kąta \(BSC\) jest równa \(\alpha\), a miara kąta \(ADB\) jest równa \(\gamma\) (zobacz rysunek).





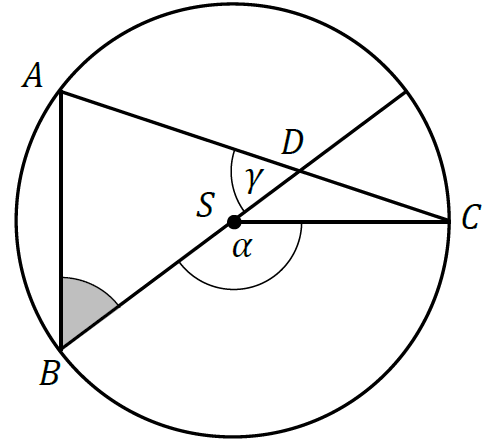
Wtedy kąt \(ABD\) ma miarę:

A \(\frac{\alpha}{2}+\gamma-180°\)
B \(180°-\frac{\alpha}{2}-\gamma\)
C \(180°-\alpha-\gamma\)
D \(\alpha+\gamma-180°\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Wyznaczenie miary kąta \(BAC\). Powinniśmy dostrzec, że kąt środkowy \(BSC\) o mierze \(\alpha\) jest oparty na tym samym łuku co kąt wpisany \(BAC\). Skoro tak, to miara kąta \(BAC\) będzie połową kąta środkowego, czyli \(|\sphericalangle BAC|=\frac{\alpha}{2}\). Krok 2. Wyznaczenie miary kąta \(ABD\). Spójrzmy na trójkąt \(BDA\). Znamy już dwie miary kątów w tym trójkącie, a trzeci jest tym przez nas poszukiwanym. Skoro więc suma kątów w trójkącie jest równa \(180°\), to: $$|\sphericalangle ABD|=180°-\frac{\alpha}{2}-\gamma$$

Teoria:      
W trakcie opracowania