Przyprostokątna \(BC\) trójkąta prostokątnego \(ABC\) ma długość \(5\). Wysokość \(CD\) tego trójkąta, opuszczona na przeciwprostokątną, jest równa \(4\), a długość odcinka \(BD\) jest równa \(3\) (jak na rysunku).





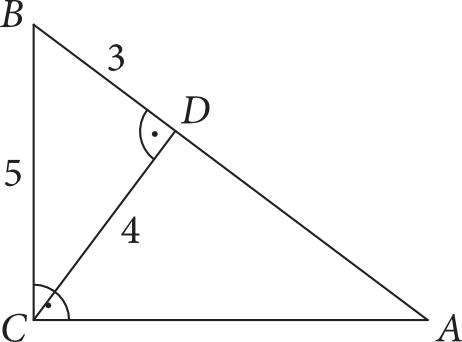
Pole trójkąta \(ABC\) jest równe:

A \(16\frac{2}{3}\)
B \(18\frac{3}{4}\)
C \(33\frac{1}{3}\)
D \(36\frac{3}{5}\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Powinniśmy dostrzec, że trójkąty \(BCD\) oraz \(CAD\) są trójkątami podobnymi. Skąd to wiemy? Jeżeli kąt \(CBD\) oznaczymy sobie jako \(\alpha\), to kąt \(BCD\) ma miarę \(90°-\alpha\). To z kolei prowadzi nas do wniosku, że skoro kąt \(BCA\) jest kątem prostym, to miara kąta \(DCA\) będzie równa: $$|\sphericalangle DCA|=90°-|\sphericalangle BCD| \           ,\ |\sphericalangle DCA|=90°-(90°-\alpha) \           ,\ |\sphericalangle DCA|=\alpha$$ Skoro \(|\sphericalangle DCA|=\alpha\) to kąt \(CAD\) ma miarę \(90°-\alpha\), czyli taką jak kąt \(BCD\). Krok 2. Obliczenie skali podobieństwa. Zastanówmy się teraz jaka jest skala podobieństwa tych trójkątów. Szukamy długości boków odpowiadających i widzimy, że taką parę stanowią jedne z przyprostokątnych tych dwóch trójkątów, czyli \(BD\) oraz \(DC\), które mają długości równe \(3\) oraz \(4\). Przyjmując, że trójkąt \(CAD\) jest trójkątem podobnym do \(BCD\) możemy zapisać, że w takim razie skala podobieństwa wynosi \(k=\frac{4}{3}\). Krok 3. Obliczenie pola powierzchni trójkąta \(BCD\). Zanim wykorzystamy własności trójkątów podobnych, to obliczmy miarę trójkąta \(BCD\). Znamy wszystkie miary tego trójkąta, więc nie będzie z tym żadnego problemu: $$P_{BCD}=\frac{1}{2}\cdot4\cdot3 \           ,\ P_{BCD}=6$$ Krok 4. Obliczenie pola powierzchni trójkąta \(CAD\). Z własności trójkątów podobnych wiemy, że przy skali podobieństwa równej \(k\), trójkąt podobny ma pole powierzchni \(k^2\) razy większe od trójkąta podstawowego. Skoro tak, to: $$P_{CAD}=k^2\cdot P_{BCD} \           ,\ P_{CAD}=\left(\frac{4}{3}\right)^2\cdot6 \           ,\ P_{CAD}=\frac{16}{9}\cdot6 \           ,\ P_{CAD}=\frac{96}{9}=10\frac{6}{9}=10\frac{2}{3}$$ Krok 5. Obliczenie pola powierzchni trójkąta \(ABC\). Na koniec została już tylko formalność, bowiem suma pól trójkątów \(BCD\) oraz \(CAD\) daje nam poszukiwane pole powierzchni trójkąta \(ABC\): $$P_{ABC}=P_{BCD}+P_{CAD} \           ,\ P_{ABC}=6+10\frac{2}{3} \           ,\ P_{ABC}=16\frac{2}{3}$$

Teoria:      
W trakcie opracowania