Rozważmy bryłę powstałą w następujący sposób: w walcu, którego wysokość jest równa \(4\), a promień podstawy \(2\), wydrążono stożek o podstawie pokrywającej się z górną podstawą walca i wierzchołku leżącym w odległości \(1\) od dolnej podstawy walca (jak na rysunku).





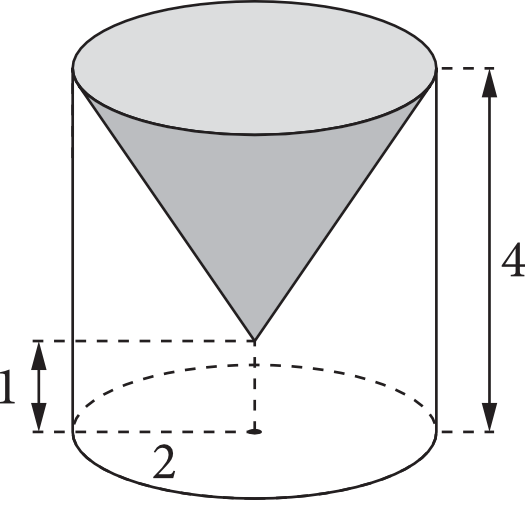
Objętość powstałej bryły jest równa:

A \(16\pi\)
B \(12\pi\)
C \(6\pi\)
D \(4\pi\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Obliczenie objętości stożka. Na początek obliczmy objętość wydrążonego stożka. Wiemy, że \(r=2\) oraz \(H=3\), zatem: $$V_{s}=\frac{1}{3}\cdot P_{p}\cdot H \           ,\ V_{s}=\frac{1}{3}\cdot2^2\cdot\pi\cdot3 \           ,\ V_{s}=\frac{1}{3}\cdot4\pi\cdot3 \           ,\ V_{s}=4\pi$$ Krok 2. Obliczenie objętości walca. Teraz obliczmy objętość walca, podstawiając do stosownego wzoru \(r=2\) oraz \(H=4\): $$V_{w}=P_{p}\cdot H \           ,\ V_{w}=2^2\cdot\pi\cdot4 \           ,\ V_{w}=4\pi\cdot4 \           ,\ V_{w}=16\pi$$ Krok 3. Obliczenie objętości powstałej bryły. Interesująca nas objętość bryły będzie różnicą między objętością walca i stożka, zatem: $$V=V_{w}-V_{s} \           ,\ V=16\pi-4\pi \           ,\ V=12\pi$$

Teoria:      
W trakcie opracowania