Punkty \(A, B, C\) i \(D\) leżą na okręgu o środku \(S\). Odcinek \(BD\) jest średnicą tego okręgu, a miary kątów \(ADC\) i \(CAD\), wpisanych w ten okrąg, są równe odpowiednio \(110°\) i \(28°\) (jak na rysunku).





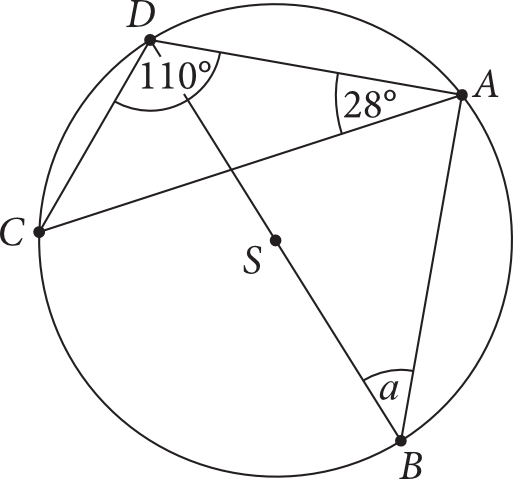
Miara \(\alpha\) kąta wpisanego \(ABD\) jest równa:

A \(14°\)
B \(28°\)
C \(42°\)
D \(56°\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(DCA\). Spójrzmy na trójkąt \(CAD\). Znamy miary dwóch kątów tego trójkąta, zatem i trzecią obliczymy bez problemu: $$|\sphericalangle DCA|=180°-110°-28° \           ,\ |\sphericalangle DCA|=42°$$ Krok 2. Wyznaczenie miary kąta \(\alpha\). Jeżeli się dobrze przyjrzymy, to zauważymy, że zarówno kąt \(DCA\) jak i kąt \(\alpha\) są kątami wpisanymi, które są oparte na tym samym łuku. Z własności kątów wpisanych wiemy, że w takiej sytuacji miara kątów jest jednakowa, stąd też \(\alpha=42°\).

Teoria:      
W trakcie opracowania