Przez punkt przecięcia wysokości trójkąta równobocznego \(ABC\) poprowadzono prostą \(DE\) równoległą do podstawy \(AB\) (zobacz rysunek).





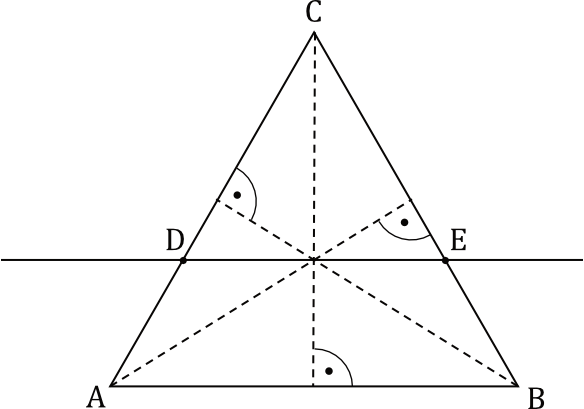
Stosunek pola trójkąta \(ABC\) do pola trójkąta \(CDE\) jest równy:

A \(9:4\)
B \(4:1\)
C \(4:9\)
D \(3:2\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Dostrzeżenie trójkątów podobnych i wykorzystanie własności trójkątów równobocznych. Powinniśmy dostrzec, że skoro prosta \(DE\) jest równoległą do podstawy \(AB\), to trójkąt \(DEC\) jest podobny do trójkąta \(ABC\). Dodatkowo z własności trójkątów równobocznych wiemy, że odległość od punktu przecięcia się wysokości aż do wierzchołka, stanowi \(\frac{2}{3}h\). Skoro tak i skoro trójkąty \(ABC\) oraz \(DEC\) są podobne, to analogicznie podstawa \(DE\) będzie stanowić \(\frac{2}{3}\) długości podstawy \(AB\). Z naszych analiz wynika więc, że mamy taką oto sytuację: Krok 2. Obliczenie pola powierzchni trójkątów \(ABC\) oraz \(DEC\). Ze wzoru na pole trójkąta możemy zapisać, że: $$P_{ABC}=\frac{1}{2}ah \           ,\ \text{oraz} \           ,\ P_{DEC}=\frac{1}{2}\cdot\frac{2}{3}a\cdot\frac{2}{3}h \           ,\ P_{DEC}=\frac{4}{18}ah$$ Krok 3. Obliczenie stosunku pól powierzchni trójkątów \(ABC\) oraz \(DEC\). Interesuje nas stosunek pól tych dwóch trójkątów, zatem: $$\frac{P_{ABC}}{P_{DEC}}=\frac{\frac{1}{2}ah}{\frac{4}{18}ah}=\frac{\frac{1}{2}}{\frac{4}{18}}=\frac{1}{2}:\frac{4}{18}=\frac{1}{2}\cdot\frac{18}{4}=\frac{18}{8}=\frac{9}{4}$$ To oznacza, że stosunek tych dwóch pól jest równy \(9:4\).

Teoria:      
W trakcie opracowania