Zaznaczone na rysunku kąty \(\alpha, \beta, \gamma\) mają miary:

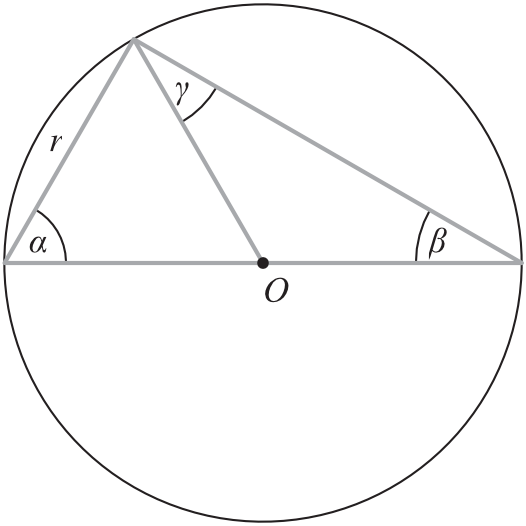
A \(\alpha=60°, \beta=30°, \gamma=30°\)
B \(\alpha=50°, \beta=40°, \gamma=40°\)
C \(\alpha=70°, \beta=20°, \gamma=20°\)
D \(\alpha=30°, \beta=60°, \gamma=60°\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Powinniśmy zauważyć, że jeden z boków trójkąta opiera się na średnicy okręgu, a to pozwala nam stwierdzić, że cały duży trójkąt (nazwijmy go \(ABC\)) jest prostokątny. Krok 2. Obliczenie miary kąta \(\alpha\). Zwróćmy uwagę, że trójkąt \(AOB\) z zaznaczonym kątem \(\alpha\) jest równoboczny, czyli każdy kąt tego trójkąta ma miarę \(60°\). Skąd to wiemy? Widzimy wyraźnie, że każdy bok tego trójkąta ma jednakową długość promienia i właśnie ta obserwacja pozwala nam błyskawicznie wyznaczyć, że \(\alpha=60°\). Teoretycznie moglibyśmy już zakończyć rozwiązywanie tego zadania (bo pasuje już tylko jedna odpowiedź), ale spróbujmy jeszcze samodzielnie obliczyć pozostałe miary kątów. Krok 3. Obliczenie miar kątów \(\beta\) oraz \(\gamma\). Skoro kąt \(ACB\) ma miarę \(90°\), a kąt \(ACO\) ma miarę \(60°\), to kąt \(\gamma\) będzie mieć miarę: $$\gamma=90°-60°=30°$$ Trójkąt \(OBC\) jest równoramienny (ramiona \(OB\) oraz \(OC\) mają długość równą promieniowi okręgu), a skoro tak, to kąty przy boku \(BC\) muszą mieć jednakową miarę. W związku z tym możemy stwierdzić, że \(\beta=30°\).

Teoria:      
W trakcie opracowania