Punkt \(O\) jest środkiem okręgu o średnicy \(AB\) (tak jak na rysunku). Kąt \(α\) ma miarę:

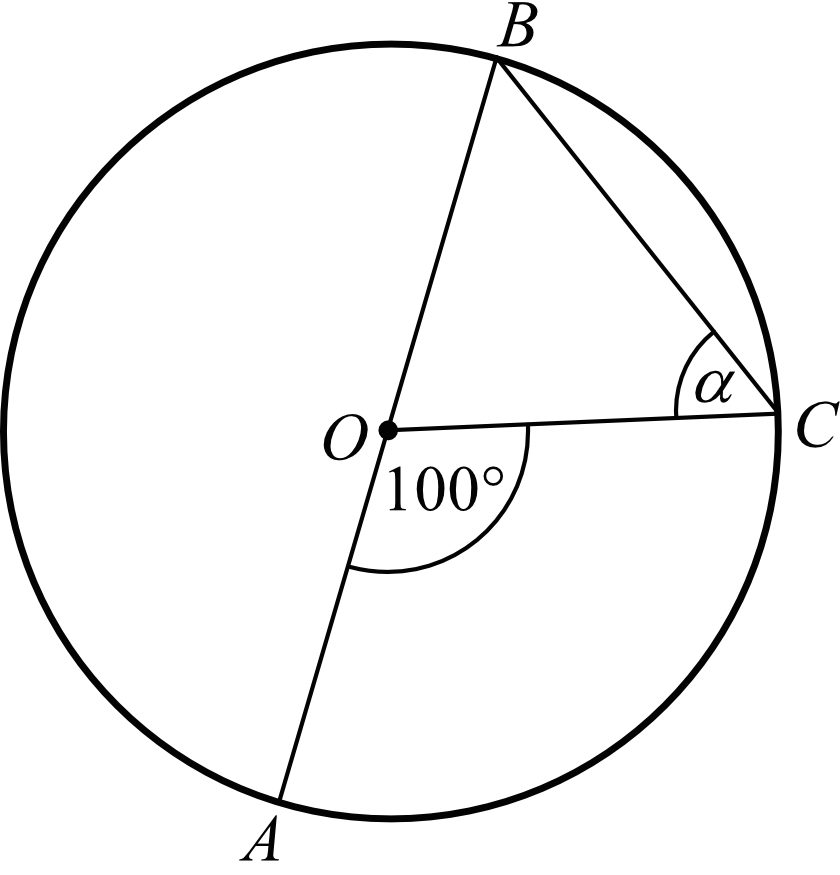
A \(40°\)
B \(50°\)
C \(60°\)
D \(80°\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(BOC\). Kąty \(BOC\) oraz \(AOC\) są kątami przyległymi, a więc takimi których łączna miara jest równa \(180°\). Zatem: $$|\sphericalangle BOC|=180°-100°=80°$$ Krok 2. Obliczenie miary kąta \(α\). Musimy zauważyć, że odcinki \(BO\) oraz \(CO\) są jednakowej długości (dokładnie jest to promień okręgu). To oznacza, że trójkąt \(OCB\) jest równoramienny o podstawie \(BC\). Z własności trójkątów równoramiennych wiemy, że kąty przy podstawie mają taką samą miarę, więc: $$80°+2α=180° \           ,\ 2α=100° \           ,\ α=50°$$

Teoria:      
W trakcie opracowania