Przyprostokątna AC trójkąta prostokątnego ABC ma długość 6, a wysokość CD dzieli go na dwa takie trójkąty ADC i CDB, że pole trójkąta ADC jest 4 razy większe od pola trójkąta CDB (zobacz rysunek).





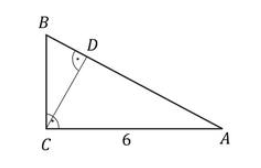
Przyprostokątna BC trójkąta prostokątnego ABC jest równa:

A 1,5
B 2
C 2,5
D 3

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie skali podobieństwa trójkątów. Z własności podobieństwa wynika, że jeżeli jakiś trójkąt jest podobny do drugiego w skali podobieństwa równej \(k\), to pole tego trójkąta będzie \(k^2\) razy większe. W naszym przypadku pole trójkąta \(ADC\) jest \(4\) razy większe od trójkąta \(CDB\), zatem: $$k^2=4 \           ,\ k=2 \quad\lor\quad k=-2$$ Skala podobieństwa nie może być ujemna, zatem zostaje nam \(k=2\). Krok 2. Obliczenie długości przyprostokątnej \(BC\). Wiemy już, że skala podobieństwa jest równa \(k=2\), czyli że wszystkie boki trójkąta \(ADC\) są dwa razy większe od analogicznych boków trójkąta \(CDB\). Bok \(BC\) jest przeciwprostokątną trójkąta \(CDB\), tak samo jak bok \(CA\) jest przeciwprostokątną trójkąta \(ADC\). Skoro tak, to bok \(BC\) będzie dwa razy krótszy od boku \(CA\), czyli \(|BC|=3\).

Teoria:      
W trakcie opracowania