Na rysunku poniżej przedstawiono fragment wykresu funkcji kwadratowej \(f\) określonej wzorem \(f(x)=ax^2+bx+c\).





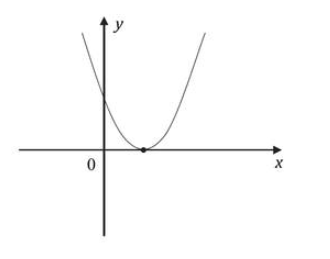
Stąd wynika, że:

A \(\begin{cases}a\lt0 \\ c\lt0 \end{cases}\)
B \(\begin{cases}a\lt0 \\ c\gt0 \end{cases}\)
C \(\begin{cases}a\gt0 \\ c\lt0 \end{cases}\)
D \(\begin{cases}a\gt0 \\ c\gt0 \end{cases}\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Ustalenie wartości współczynnika \(a\). Współczynnik \(a\) informuje nas o kierunku ułożenia ramion paraboli. W naszym przypadku ramiona paraboli są skierowane do góry, a to oznacza, że \(a\gt0\). Krok 2. Ustalenie wartości współczynnika \(c\). Współczynnik \(c\) informuje nas o miejscu przecięcia się wykresu z osią \(OY\). Możemy powiedzieć, że parabola przecina oś w punkcie \(P=(0;c)\). Podana na rysunku parabola przecina oś \(OY\) dla dodatniej wartości (czyli nad osią iksów), zatem \(c\gt0\). To oznacza, że obydwa współczynniki są dodatnie, czyli że \(\begin{cases}a\gt0 \\ c\gt0 \end{cases}\).

Teoria:      
W trakcie opracowania