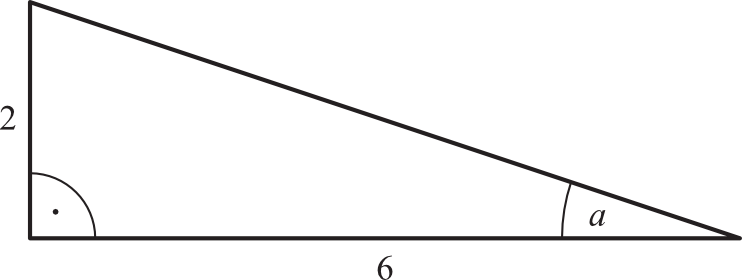
W trójkącie przedstawionym na rysunku sinus kąta ostrego \(α\) jest równy:

A \(\frac{1}{3}\)
B \(3\)
C \(\sqrt{10}\)
D \(\frac{\sqrt{10}}{10}\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie długości przeciwprostokątnej trójkąta. Do obliczenia sinusa potrzebujemy poznać długość przeciwprostokątnej trójkąta, a poznamy ją korzystając z Twierdzenia Pitagorasa: $$a^2+b^2=c^2 \           ,\ 2^2+6^2=c^2 \           ,\ 4+36=c^2 \           ,\ c^2=40 \           ,\ c=\sqrt{40} \quad\lor\quad c=-\sqrt{40}$$ Ujemny wynik oczywiście odrzucamy, bo długość przeciwprostokątnej jest dodatnia. To oznacza, że \(c=\sqrt{40}\), co po wyłączeniu czynnika przed znak pierwiastka możemy jeszcze zapisać jako: $$c=\sqrt{40}=\sqrt{4\cdot10}=2\sqrt{10}$$ Krok 2. Obliczenie wartości sinusa. Sinus odpowiada stosunkowi długości przyprostokątnej leżącej naprzeciwko kąta do długości przeciwprostokątnej, zatem: $$sinα=\frac{2}{2\sqrt{10}} \           ,\ sinα=2:2\sqrt{10} \           ,\ sinα=2\cdot\frac{1}{2\sqrt{10}} \           ,\ sinα=\frac{1}{\sqrt{10}}$$ Nasz wynik jest już poprawny, ale aby dopasować się do odpowiedzi musimy jeszcze usunąć niewymierność z mianownika, mnożąc licznik i mianownik przez \(\sqrt{10}\): $$sinα=\frac{1\cdot\sqrt{10}}{\sqrt{10}\cdot\sqrt{10}} \           ,\ sinα=\frac{\sqrt{10}}{10}$$

Teoria:      
W trakcie opracowania