W trójkącie równoramiennym \(ABC\), w którym \(AC=BC\) poprowadzono dwusieczne kątów \(ABC\) i \(ACB\). Dwusieczne te przecięły się w punkcie \(O\) (patrz rysunek).





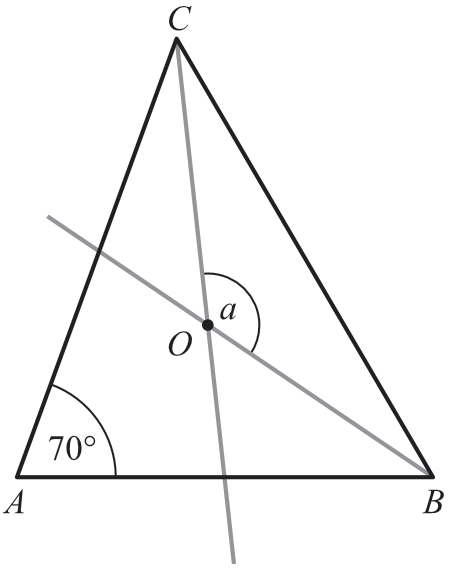
Jeśli \(|\sphericalangle BAC|=70°\), to miara kąta \(α\) jest równa:

A \(140°\)
B \(110°\)
C \(55°\)
D \(125°\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Wyznaczenie miary kąta \(OBC\). Z treści zadania wynika, że nasz trójkąt jest równoramienny, a skoro tak, to kąty przy jego podstawie będą miały jednakową miarę. To z kolei oznacza, że kąt \(|\sphericalangle ABC|=70°\). Przez ten kąt \(ABC\) poprowadzono dwusieczną kąta, zatem: $$|\sphericalangle OBC|=70°:2 \           ,\ |\sphericalangle OBC|=35°$$ Krok 2. Wyznaczenie miary kąta \(COB\). Skoro kąty przy podstawie mają po \(70°\), to: $$|\sphericalangle ACB|=180°-70°-70°=40°$$ Przez ten kąt poprowadzono dwusieczną kąta, zatem: $$|\sphericalangle COB|=40°:2 \           ,\ |\sphericalangle COB|=20°$$ Krok 3. Wyznaczenie miary kąta \(α\). Spójrzmy na trójkąt \(COB\). Znamy już miary dwóch kątów w tym trójkącie, zatem: $$α=180°-35°-20° \           ,\ α=125°$$

Teoria:      
W trakcie opracowania