Na rysunkach I-IV przedstawiono cztery pary trójkątów.





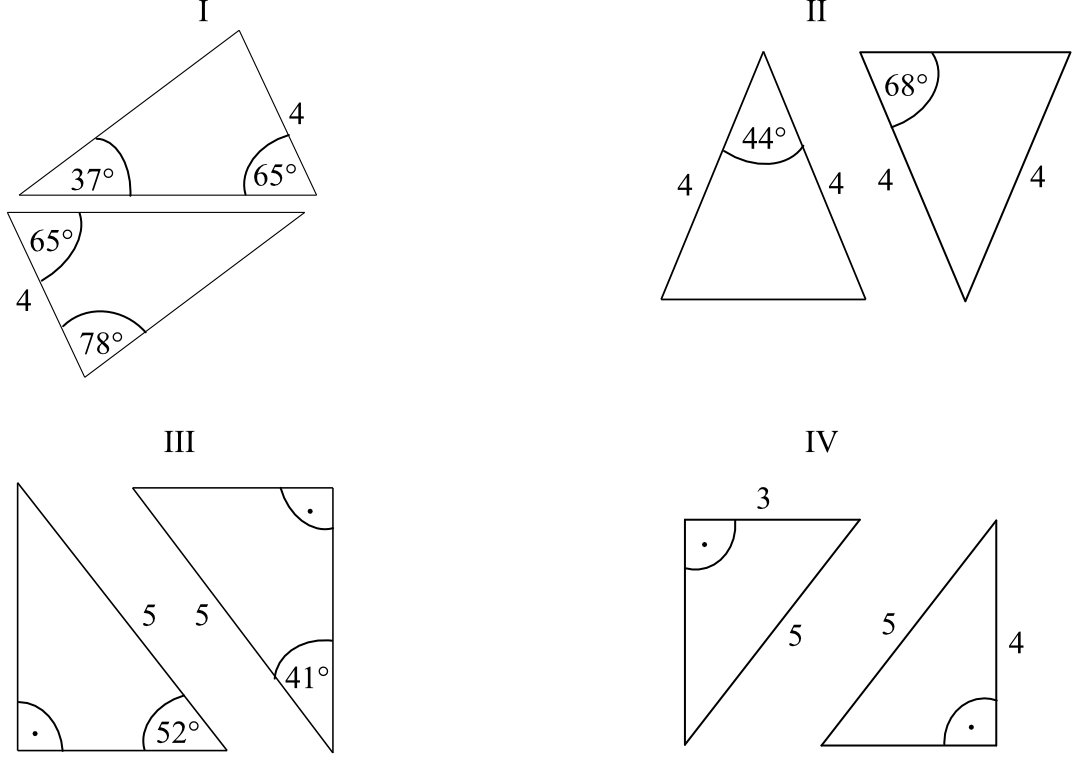
Na którym rysunku trójkąty nie są przystające?

A I
B II
C III
D IV

Odpowiedź:      

C

Rozwiązanie:      
Przeanalizujmy każdą parę trójkątów: Para I: Miara trzeciego kąta górnego trójkąta jest równa: \(180°-37°-65°=78°\) Miara trzeciego kąta dolnego trójkąta jest równa: \(180°-78°-65°=37°\) To oznacza, że te trójkąty mają jednakowe miary wszystkich kątów, zatem są podobne na podstawie cechy kąt-kąt-kąt. Para II: Mamy trójkąty równoramienne, więc kąty przy podstawie muszą mieć jednakową miarę. Skoro tak, to w trójkącie po lewej stronie kąty przy podstawie mają łączną miarę \(180°-44°=136°\), a skoro są to kąty o jednakowej mierze to każdy z nich ma \(136°:2=68°\). Trójkąt po prawej stronie jest także równoramienny, więc kąty przy podstawie mają jednakowe miary, czyli będzie to \(68°\) oraz \(68°\), a to z kolei oznacza, że trzeci kąt ma miarę: \(180°-68°-68°=44°\). Wyszło nam więc, że te trójkąty są podobne zgodnie z cechą kąt-kąt-kąt. Para III: Trzeci kąt trójkąta po lewej stronie ma miarę: \(180°-90°-52°=38°\). Trzeci kąt trójkąta po prawej stronie ma miarę: \(180°-90°-41°=49°\). Te trójkąty nie mają jednakowych miar kątów, więc nie są trójkątami podobnymi Para IV: Trójkąt po lewej stronie ma znane wymiary \(3\) oraz \(5\). Brakuje nam długości jednego z boków, ale widząc że jest to trójkąt prostokątny możemy skorzystać z Twierdzenia Pitagorasa: $$3^2+b^2=5^2 \           ,\ 9+b^2=25 \           ,\ b^2=16 \           ,\ b=4$$ Analogiczna sytuacja jest w trójkącie po prawej stronie: $$a^2+4^2=5^2 \           ,\ a^2+16=25 \           ,\ a^2=9 \           ,\ a=3$$ To oznacza, że te trójkąty są podobne, bo mają jednakowe długości wszystkich boków (cecha bok-bok-bok). Ostatecznie z naszej analizy wynika, że trójkąty przystające nie znalazły się jedynie na trzecim rysunku.

Teoria:      
W trakcie opracowania