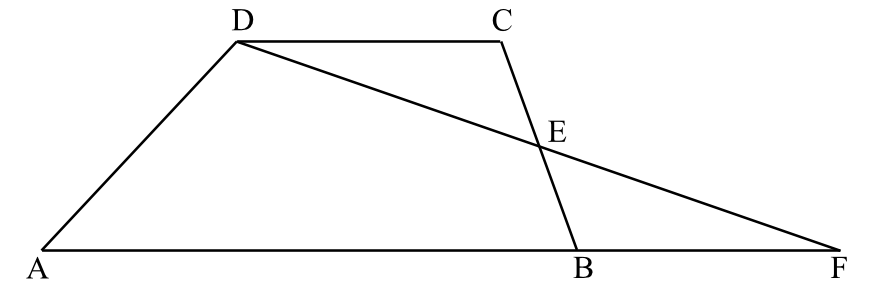
Na rysunku przedstawiono trapez \(ABCD\) i trójkąt \(AFD\). Punkt \(E\) leży w połowie odcinka \(BC\). Uzasadnij, że pole trapezu \(ABCD\) i pole trójkąta \(AFD\) są równe.

Odpowiedź:      

Udowodniono wykorzystując własności trójkątów przystających.

Rozwiązanie:      
Krok 1. Rozpisanie pól powierzchni. Spójrzmy najpierw na pole trapezu \(ABCD\). Jest on sumą pól czworokąta \(ABED\) oraz trójkąta \(ECD\). Możemy więc zapisać, że: $$P_{ABCD}=P_{ABED}+P_{ECD}$$ Teraz spójrzmy na trójkąt \(AFD\). Tutaj także jedną z części składowych jest czworokąt \(ABED\) oraz trójkąt \(BFE\): $$P_{AFD}=P_{ABED}+P_{BFE}$$ Skoro tak, to wystarczyłoby udowodnić że trójkąty \(ECD\) oraz \(BFE\) są trójkątami przystającymi, czyli że mają jednakowe wymiary i pole powierzchni. Krok 2. Sporządzenie rysunku pomocniczego i przeprowadzenie dowodzenia. Spróbujmy wprowadzić oznaczenia kątów na naszym rysunku: Kąty \(CED\) oraz \(FEB\) są kątami wierzchołkowymi, więc na pewno mają tą samą miarę. Kąty \(EBF\) oraz \(ECD\) to kąty naprzemianległe, więc także mają jednakową miarę. Dodatkowo z treści zadania wiemy, że \(|CE|=|EB|\). Na podstawie tych informacji możemy stwierdzić, że trójkąty \(ECD\) oraz \(BFE\) są trójkątami przystającymi na podstawie cechy przystawania trójkątów kąt-bok-kąt. Skoro są to trójkąty przystające to miara ich pól powierzchni jest jednakowa, co ostatecznie powoduje że \(P_{ABCD}=P_{AFD}\).

Teoria:      
W trakcie opracowania