Janek otrzymał z kartkówki ocenę dostateczną, czyli \(3\). Postanowił porównać tę ocenę ze średnią ocen klasy z tego sprawdzianu. W tym celu przeanalizował diagram, na którym przedstawiono wyniki wszystkich uczniów tej klasy.





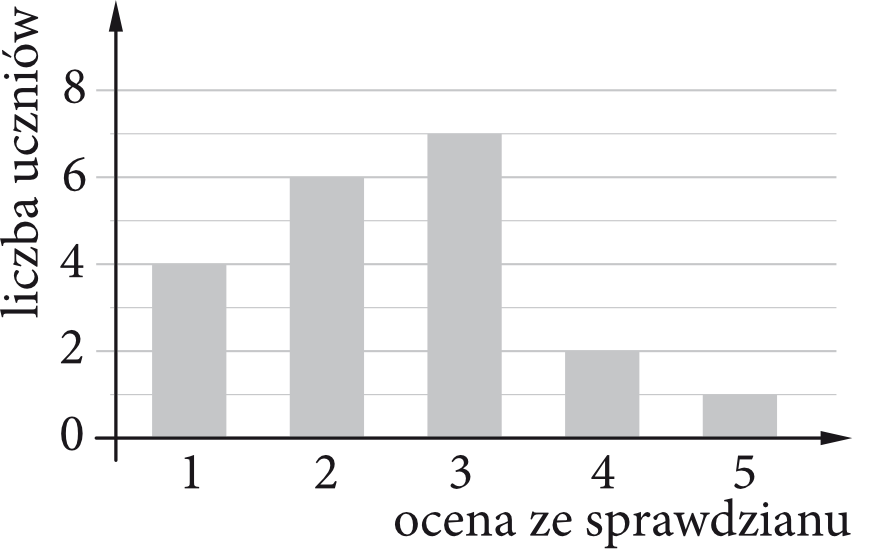
O ile ocena, którą uzyskał Janek, była wyższa niż średnia ocen klasy?

Odpowiedź:      

Ocena Janka była wyższa niż średnia klasy o \(0,5\) stopnia.

Rozwiązanie:      
Krok 1. Obliczenie średniej ocen z kartkówki. Z wykresu możemy odczytać, że: • \(4\) uczniów otrzymało jedynkę • \(6\) uczniów otrzymało dwójkę • \(7\) uczniów otrzymało trójkę • \(2\) uczniów otrzymało czwórkę • \(1\) uczeń otrzymał piątkę To oznacza, że średnia ocen uczniów wyniosła: $$śr=\frac{4\cdot1+6\cdot2+7\cdot3+2\cdot4+1\cdot5}{4+6+7+2+1} \           ,\ śr=\frac{4+12+21+8+5}{20} \           ,\ śr=\frac{50}{20} \           ,\ śr=2,5$$ Krok 2. Obliczenie o ile ocena, którą uzyskał Janek, była wyższa niż średnia ocen. Janek otrzymał ocenę \(3\). Średnia klasy wyniosła \(2,5\). To oznacza, że ocena Janka jest wyższa od średniej ocen całej klasy o \(3-2,5=0,5\) stopnia.

Teoria:      
W trakcie opracowania