Prostokąt o bokach długości \(8cm\) i \(30cm\) (rysunek 1) rozcięto na cztery przystające trójkąty, a następnie z tych trójkątów ułożono figurę, jak pokazano na rysunku 2.





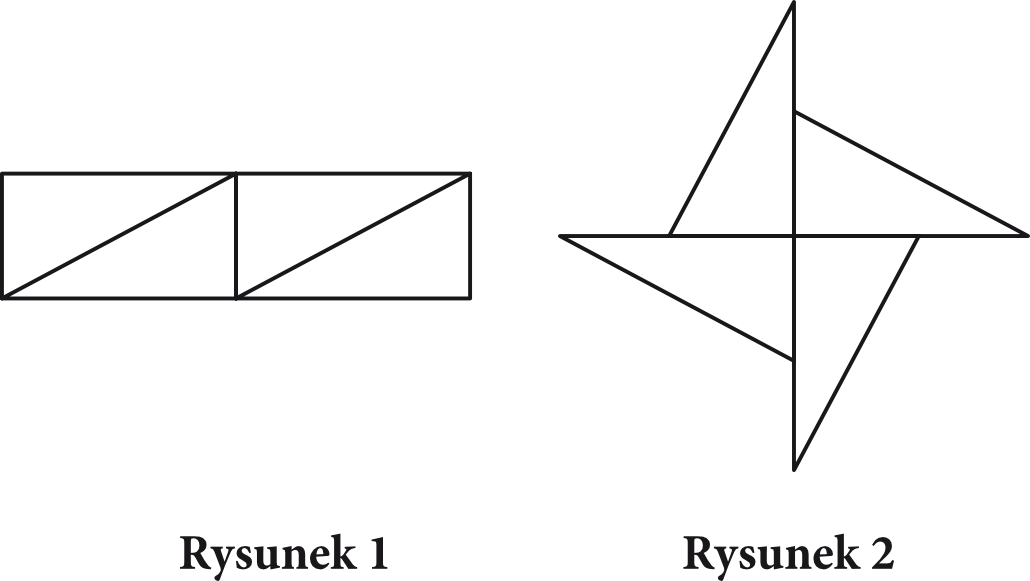
Ile wynosi obwód figury przedstawionej na rysunku 2?

Odpowiedź:      

\(Obw=96cm\)

Rozwiązanie:      
Krok 1. Obliczenie długości przyprostokątnych oraz przeciwprostokątnej trójkąta. Prostokąt został podzielony na cztery przystające (czyli jednakowe) trójkąty prostokątne. Spróbujmy poznać wymiary każdego z tych trójkątów. Ustalmy najpierw jakie są długości przyprostokątnych tego trójkąta. Z rysunku wynika, że \(a=8cm\) (bo krótsza przyprostokątna pokrywa się z krótszym bokiem prostokąta), natomiast \(b=15cm\) (bo dłuższa przyprostokątna to połowa długości całego prostokąta). Znając długości przyprostokątnych możemy obliczyć długość przeciwprostokątnej, której długość potrzebujemy do obliczenia obwodu drugiej figury. Korzystając z Twierdzenia Pitagorasa możemy zapisać, że: $$8^2+15^2=c^2 \           ,\ 64+225=c^2 \           ,\ c^2=289 \           ,\ c=\sqrt{289} \quad\lor\quad c=-\sqrt{289} \           ,\ c=17 \quad\lor\quad c=-17$$ Ujemny wynik oczywiście odrzucamy, zatem zostaje nam \(c=17cm\). Krok 2. Obliczenie różnicy między dłuższą i krótszą przyprostokątną. Jak spojrzymy się na rysunek to zauważymy, że na obwód drugiej figury składają się jeszcze takie małe fragmenty, które są różnicą między długością dłuższej i krótszej przyprostokątnej. Dłuższa przyprostokątna ma długość \(15cm\), krótsza ma długość \(8cm\), zatem każdy pojedynczy mały kawałeczek obwodu tej figury będzie miał długość: $$15cm-8cm=7cm$$ Krok 3. Obliczenie obwodu figury. Nasza figura składa się z czterech odcinków o długości przeciwprostokątnej (którą wyznaczyliśmy w 1. kroku) oraz czterech odcinków o długości będącej różnicą między przyprostokątnymi (którą wyznaczyliśmy w 2. kroku). W związku z tym: $$Obw=4\cdot17cm+4\cdot7cm=68cm+28cm=96cm$$

Teoria:      
W trakcie opracowania