Dziadek Janusz chce pomalować jedno z pomieszczeń w swoim mieszkaniu. Oszacował, że powierzchnia ścian i sufitu to łącznie prawie \(70m^2\). Z oferty sklepu wybrał wstępnie cztery rodzaje farb, które przedstawiono w poniższej tabeli.





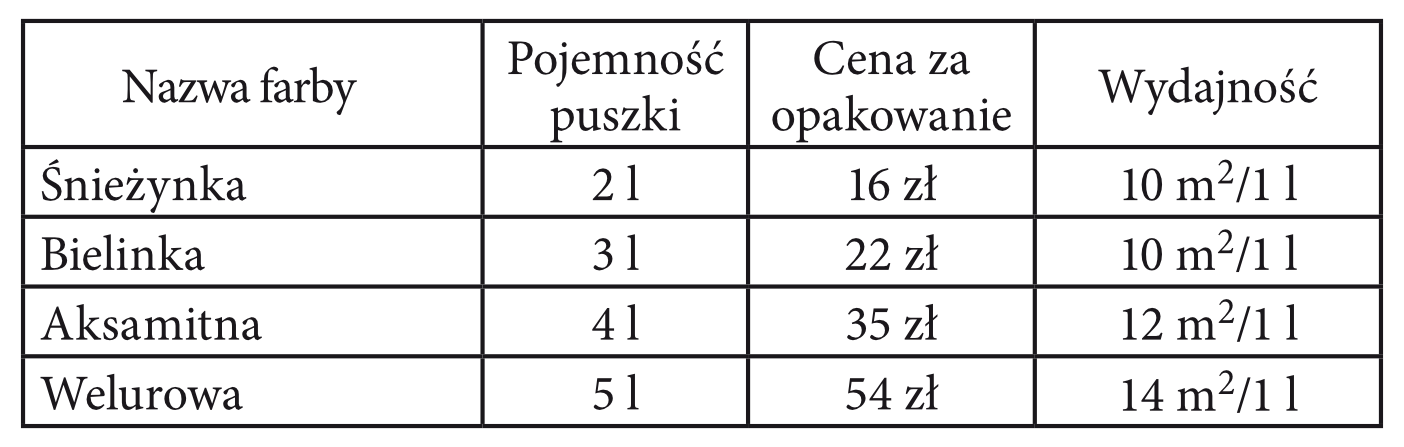
Którą farbę powinien wybrać dziadek Janusz, by dwukrotnie pomalować tę powierzchnię i wydać jak najmniej?

Odpowiedź:      

Najkorzystniej wyjdzie kupić farbę Aksamitną.

Rozwiązanie:      
Krok 1. Obliczenie ile metrów kwadratowych da się pomalować pojedynczą puszką farby. W ostatniej kolumnie mamy podaną wydajność każdej z farb w przeliczeniu na \(1\) litr. Spróbujmy zatem sprawdzić ile metrów kwadratowych pomalujemy mając każdą z wymienionych puszek. W tym celu musimy wymnożyć pojemność puszki przez jej wydajność: • Śnieżynka: \(2\cdot10\frac{m^2}{l}=20m^2\) • Bielinka: \(3\cdot10\frac{m^2}{l}=30m^2\) • Aksamitna: \(4\cdot12\frac{m^2}{l}=48m^2\) • Welurowa: \(5\cdot14\frac{m^2}{l}=70m^2\) Krok 2. Obliczenie ile puszek trzeba kupić i jaka jest ich łączna cena. Dziadek chce pomalować powierzchnię \(70m^2\) i chce to zrobić dwukrotnie, czyli realnie pomaluje \(2\cdot70m^2=140m^2\). Sprawdźmy zatem ilu puszek farby potrzeba do pomalowania takiej powierzchni i ile trzeba za nie zapłacić: • Śnieżynka - jedną puszką jesteśmy w stanie pomalować \(20m^2\), zatem tych puszek potrzebujemy: $$140m^2:20m^2=7$$ Cena pojedynczej puszki to \(16zł\), zatem malowanie Śnieżynką będzie kosztować: $$7\cdot16zł=112zł$$ • Bielinka - jedną puszką jesteśmy w stanie pomalować \(30m^2\), zatem tych puszek potrzebujemy: $$140m^2:30m^2=4\frac{2}{3}\approx5$$ Musieliśmy zaokrąglić (do góry) liczbę puszek do pełnej wartości, bo nie da się przecież kupić \(4\frac{2}{3}\) puszki. Stąd też potrzeba kupić \(5\) opakowań tej farby. Cena pojedynczej puszki to \(22zł\), zatem malowanie Bielinką będzie kosztować: $$5\cdot22zł=110zł$$ • Aksamitna - jedną puszką jesteśmy w stanie pomalować \(48m^2\), zatem tych puszek potrzebujemy: $$140m^2:48m^2=2\frac{11}{12}\approx3$$ Musieliśmy zaokrąglić (do góry) liczbę puszek do pełnej wartości, bo nie da się przecież kupić \(2\frac{11}{12}\) puszki. Stąd też potrzeba kupić \(3\) opakowania tej farby. Cena pojedynczej puszki to \(35zł\), zatem malowanie Aksamitną będzie kosztować: $$3\cdot35zł=105zł$$ • Welurowa - jedną puszką jesteśmy w stanie pomalować \(70m^2\), zatem tych puszek potrzebujemy: $$140m^2:70m^2=2$$ Cena pojedynczej puszki to \(54zł\), zatem malowanie Welurową będzie kosztować: $$2\cdot54zł=108zł$$ To oznacza, że najkorzystniej wyjdzie kupić farbę Aksamitną.

Teoria:      
W trakcie opracowania