Na rysunku przedstawiono trzy graniastosłupy: dwa o podstawie prostokąta i jeden o podstawie trapezu. Bryły te mają równe pola podstaw oraz jednakową objętość.





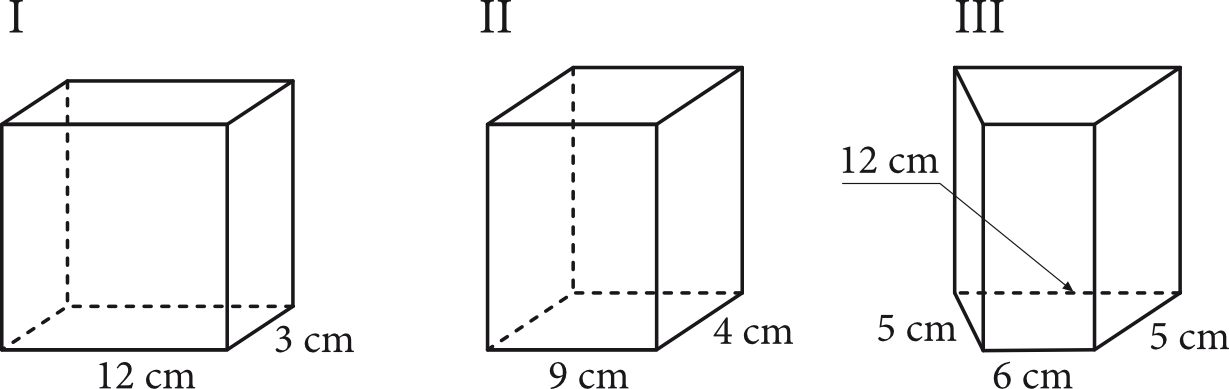
Uporządkuj pola powierzchni bocznej \(P_{I}, P_{II}\) i \(P_{III}\) tych brył od najmniejszego do największego.

A \(P_{I}\lt P_{II}\lt P_{III}\)
B \(P_{II}\lt P_{I}\lt P_{III}\)
C \(P_{III}\lt P_{II}\lt P_{I}\)
D \(P_{II}\lt P_{III}\lt P_{I}\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Dostrzeżenie, że wszystkie bryły muszą mieć jednakową wysokość. Wzór na objętość graniastosłupa to \(V=P_{p}\cdot H\). Skoro wszystkie bryły mają jednakowe pola podstawy i mają jednakową objętość, to muszą mieć także jednakową wysokość samej bryły. To ważne spostrzeżenie, bowiem dzięki temu możemy zapisać, że krawędzie boczne wszystkich brył (które są przecież wysokościami naszych graniastosłupów) mają jednakową długość \(x\). Krok 2. Obliczenie pola powierzchni bocznej pierwszej bryły. Pole powierzchni bocznej to suma pól wszystkich ścian bocznych. W przypadku pierwszej bryły ścianami bocznymi są dwa prostokąty o wymiarach \(3cm\times x\;cm\) oraz dwa prostokąty o wymiarach \(12cm\times x\;cm\). W związku z tym: $$P_{I}=2\cdot(3\cdot x)+2\cdot(12\cdot x)=6x+24x=30x$$ Krok 3. Obliczenie pola powierzchni bocznej drugiej bryły. Analogicznie jak w poprzednim przypadku, tym razem ścianami bocznymi są dwa prostokąty o wymiarach \(4cm\times x\;cm\) oraz dwa prostokąty o wymiarach \(9cm\times x\;cm\), zatem: $$P_{II}=2\cdot(4\cdot x)+2\cdot(9\cdot x)=8x+18x=26x$$ Krok 4. Obliczenie pola powierzchni bocznej trzeciej bryły. Tutaj ścianami bocznymi są dwa prostokąty o wymiarach \(5cm\times x\;cm\), jeden prostokąt o wymiarach \(6cm\times x\;cm\) oraz jeden prostokąt o wymiarach \(12cm\times x\;cm\), zatem: $$P_{III}=2\cdot(5\cdot x)+1\cdot(6\cdot x)+1\cdot(12\cdot x)=10x+6x+12x=28x$$ To oznacza, że \(P_{II}\lt P_{III}\lt P_{I}\).

Teoria:      
W trakcie opracowania