Sześcian o objętości \(1dm^3\) rozcięto na sześcienne klocki o boku długości \(1cm\), a następnie ułożono je jeden obok drugiego, tak jak przedstawiono na rysunku.





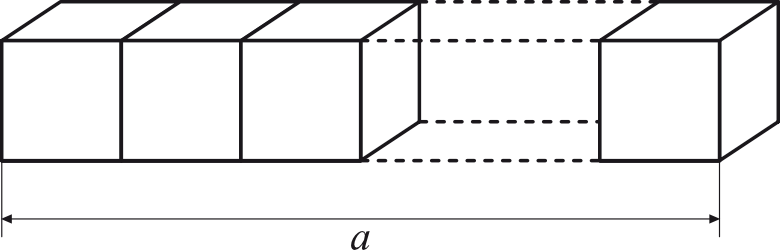
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F - jeśli jest fałszywe. Objętość powstałej bryły jest równa \(1000cm^3\).
Długość \(a\) zaznaczona na rysunku to \(10m\).

Objętość powstałej bryły jest równa \(1000cm^3\).

Odpowiedź:      

1) PRAWDA

2) PRAWDA

Rozwiązanie:      
Krok 1. Ocena prawdziwości pierwszego zdania. Niezależnie od tego jak te małe klocki zostaną ułożone, to objętość powstałej bryły będzie równa objętości początkowego sześcianu. Sześcian na początku miał objętość \(1dm^3\), zatem chcąc sprawdzić czy nowa bryła ma objętość równą \(1000cm^3\), musimy jedynie poprawnie zamienić jednostki objętości. Pamiętając o tym, że \(1dm=10cm\) możemy zapisać, że: $$1dm^3=10cm\cdot10cm\cdot10cm=1000cm^3$$ Zdanie jest więc prawdą. Krok 2. Ocena prawdziwości drugiego zdania. Musimy ustalić ile małych kostek powstało po rozcięciu naszego początkowego sześcianu. Skoro po rozcięciu powstały nam sześcienne klocki o boku \(1cm\), to każdy taki klocek ma objętość: $$V=(1cm)^3 \           ,\ V=1cm^3$$ Ustaliliśmy już, że objętość całej bryły jest równa \(1000cm^3\), więc takich małych klocków o objętości \(V=1cm^3\) jest na pewno \(1000\). To oznacza, że na rysunku mamy \(1000\) klocków ułożonych obok siebie. Każdy klocek ma długość \(1cm\), zatem długość nowej bryły będzie równa \(1000cm\), czyli właśnie \(10m\). Zdanie jest więc prawdą.

Teoria:      
W trakcie opracowania