Czworokąt \(ABCD\) jest trapezem. Podstawa \(AB\) została przedłużona do punktu \(E\). Długości niektórych odcinków w tym czworokącie opisano na rysunku.





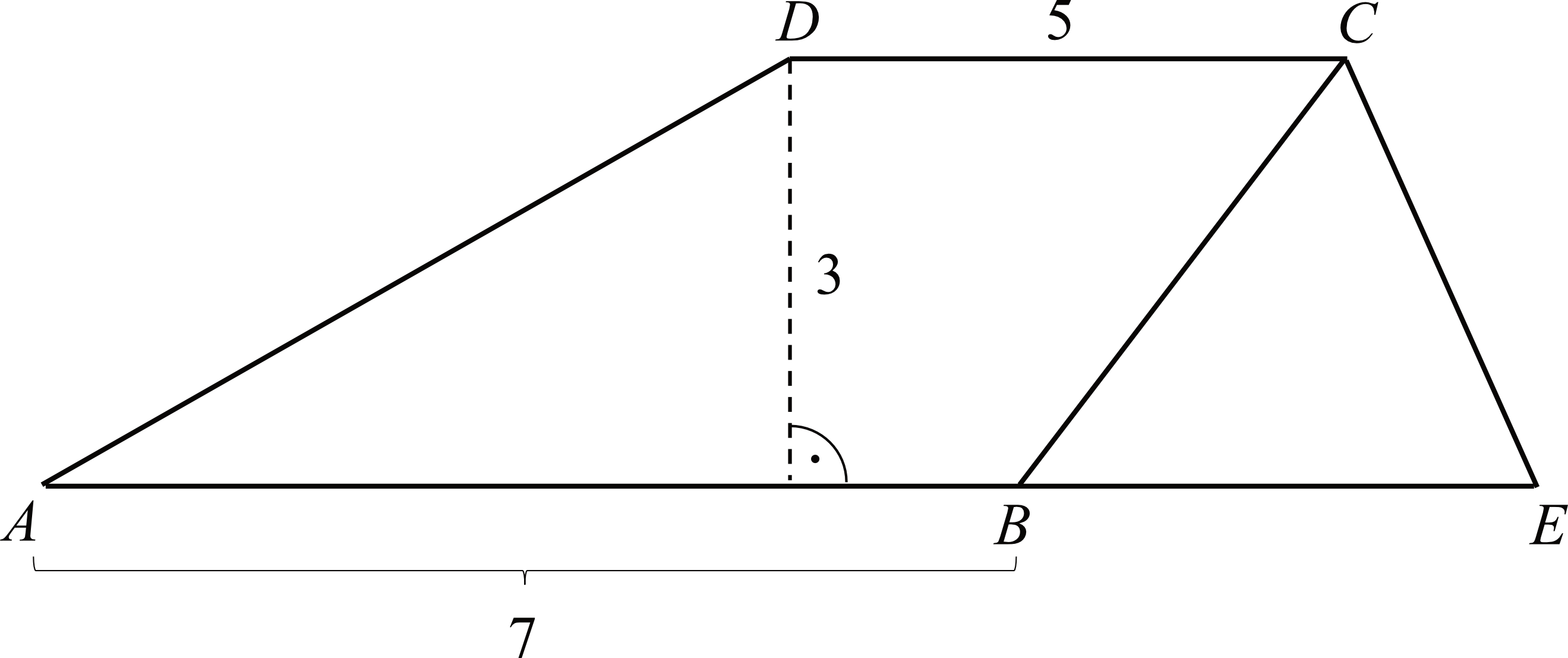
Pole trapezu \(ABCD\) jest trzy razy większe od pola trójkąta \(BEC\). Oblicz długość odcinka \(BE\). Zapisz obliczenia.

Odpowiedź:      

\(|BE|=4\)

Rozwiązanie:      
Krok 1. Obliczenie pola trapezu. Korzystając ze wzoru na pole trapezu możemy zapisać, że: $$P_{ABCD}=\frac{1}{2}\cdot(a+b)\cdot h \           ,\ P_{ABCD}=\frac{1}{2}\cdot(7+5)\cdot3 \           ,\ P_{ABCD}=\frac{1}{2}\cdot12\cdot3 \           ,\ P_{ABCD}=6\cdot3 \           ,\ P_{ABCD}=18$$ Krok 2. Obliczenie długości odcinka \(BE\). Pole trójkąta \(BEC\) jest trzy razy mniejsze, czyli \(P_{BEC}=18:3=6\). Skoro tak, to: $$P_{BEC}=\frac{1}{2}ah \           ,\ 6=\frac{1}{2}\cdot|BE|\cdot3 \           ,\ 6=1,5|BE| \           ,\ |BE|=4$$

Teoria:      
W trakcie opracowania