Dwa jednakowe prostopadłościany, każdy o wymiarach \(5 cm\), \(7 cm\) i \(9 cm\), sklejono tak, jak pokazano na rysunku.





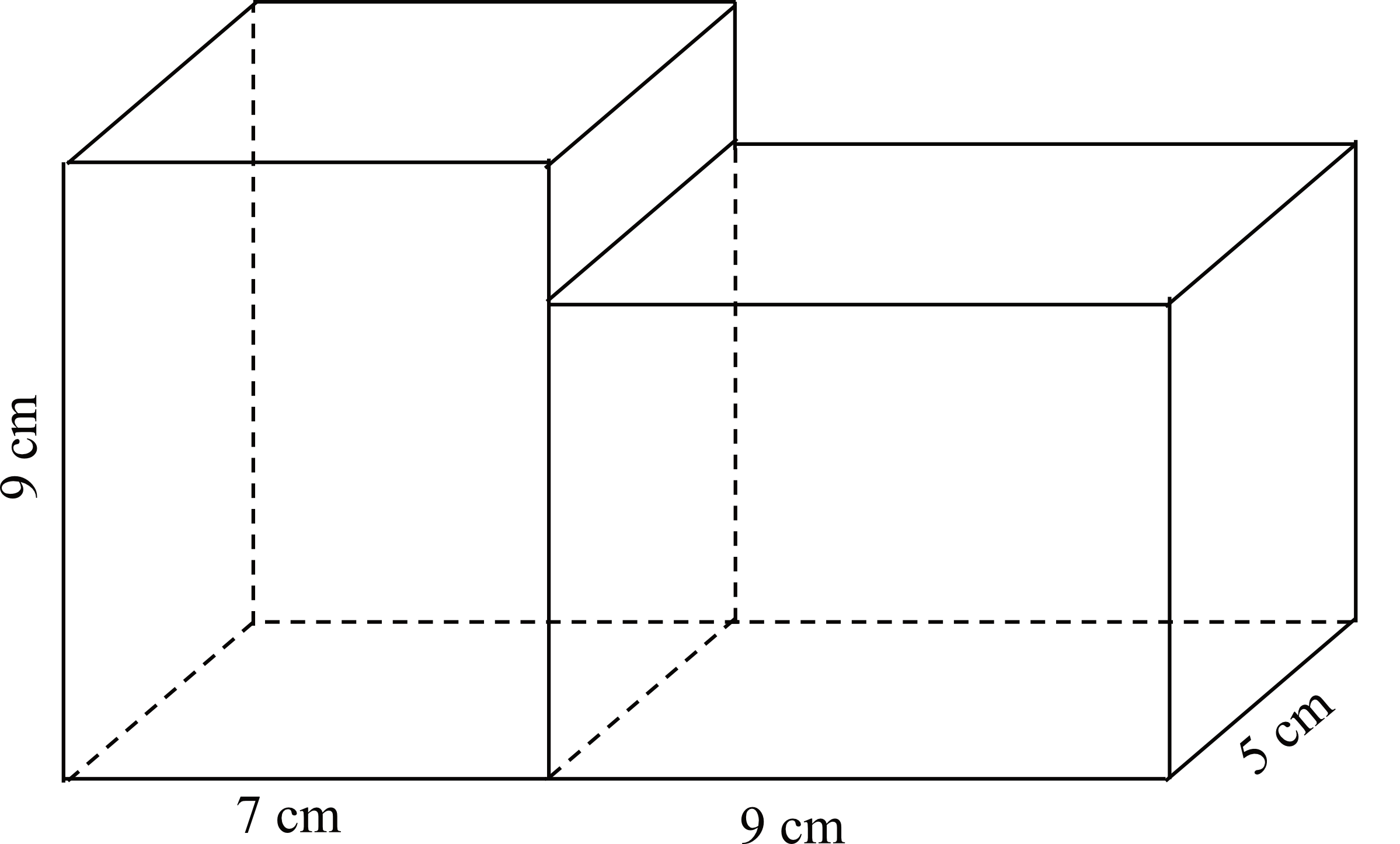
Oblicz pole powierzchni całkowitej powstałej bryły. Zapisz obliczenia.

Odpowiedź:      

\(P_{c}=502\)

Rozwiązanie:      
Krok 1. Obliczenie pola powierzchni całkowitego pojedynczego prostopadłościanu. Możemy oczywiście liczyć pole powierzchni całkowitej fragmentami (dodając pola poszczególnych ścian i ich wycinków), aczkolwiek istnieje nieco sprytniejszy sposób. Pole powierzchni całkowitej tej sklejonej bryły będzie równa polu powierzchni dwóch naszych prostopadłościanów, a całość będzie pomniejszona o pole dwóch ścian (a w zasadzie o jedną całą ścianę i jeden jej fragment), które się ze sobą stykają. Pole powierzchni pojedynczego prostopadłościanu jest równe: $$P_{c}=2\cdot(ab+ac+bc) \           ,\ P_{c}=2\cdot(5\cdot7+5\cdot9+7\cdot9) \           ,\ P_{c}=2\cdot(35+45+63) \           ,\ P_{c}=2\cdot143 \           ,\ P_{c}=286$$ Krok 2. Obliczenie pola powierzchni całkowitej powstałej bryły. Mamy dwa takie prostopadłościany, zatem suma ich pól powierzchni będzie równa \(2\cdot286cm^2=572cm^2\). Od sumy pól powierzchni dwóch prostopadłościanów musimy odjąć dwa pola powierzchni o wymiarach \(5cm\times7cm\), którymi sklejone są te dwie bryły. Pole powierzchni naszej bryły będzie więc równe: $$P_{c}=572-2\cdot5\cdot7 \           ,\ P_{c}=572-70 \           ,\ P_{c}=502$$

Teoria:      
W trakcie opracowania