Na rysunku przedstawiono czworokąt \(ABCD\), który podzielono na dwa trójkąty. Długości boków otrzymanych trójkątów opisano za pomocą wyrażeń algebraicznych. Obwód trójkąta \(ABC\) jest równy \(31\).





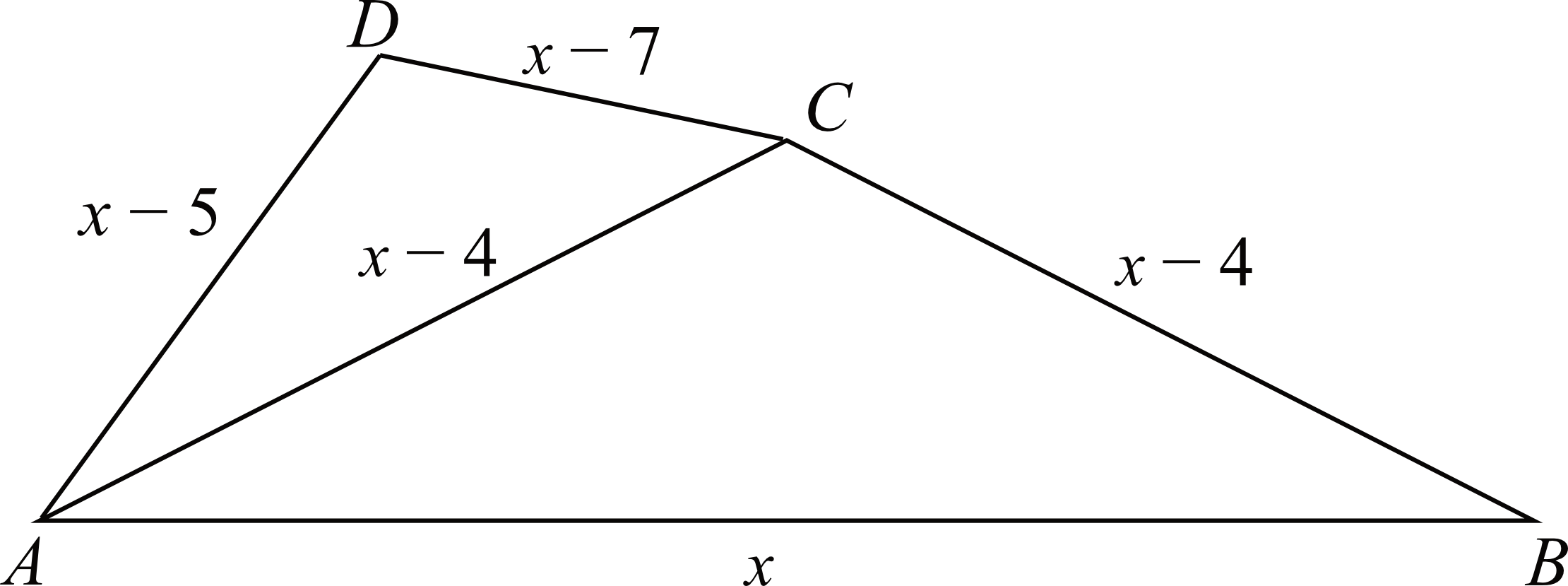
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. Odcinek \(AC\) jest o \(4\) jednostki dłuższy od odcinka \(CD\).
Obwód trójkąta \(ACD\) jest równy \(23\).

Odcinek \(AC\) jest o \(4\) jednostki dłuższy od odcinka \(CD\).

Odpowiedź:      

1) FAŁSZ

2) PRAWDA

Rozwiązanie:      
Krok 1. Ocena prawdziwości pierwszego zdania. Odcinek \(AC\) jest opisany jako \(x-4\), natomiast \(CD\) jest opisany jako \(x-7\). Widzimy więc, że zdanie jest fałszem, ponieważ różnica między tymi odcinkami wynosi \(3\) jednostki (bo \(7-4=3\)), a nie \(4\). Krok 2. Ocena prawdziwości drugiego zdania. Skoro obwód trójkąta \(ABC\) jest równy \(31\), to sumując boki trójkąta, otrzymamy następujące równanie: $$x+(x-4)+(x-4)=31 \           ,\ x+x-4+x-4=31 \           ,\ 3x-8=31 \           ,\ 3x=39 \           ,\ x=13$$ Obwód trójkąta \(ACD\) jest równy: $$Obw_{ACD}=(x-4)+(x-7)+(x-5) \           ,\ Obw_{ACD}=x-4+x-7+x-5 \           ,\ Obw_{ACD}=3x-16$$ Skoro \(x=13\), to: $$Obw_{ACD}=3\cdot13-16 \           ,\ Obw_{ACD}=39-16 \           ,\ Obw_{ACD}=23$$ Zdanie jest więc prawdą.

Teoria:      
W trakcie opracowania