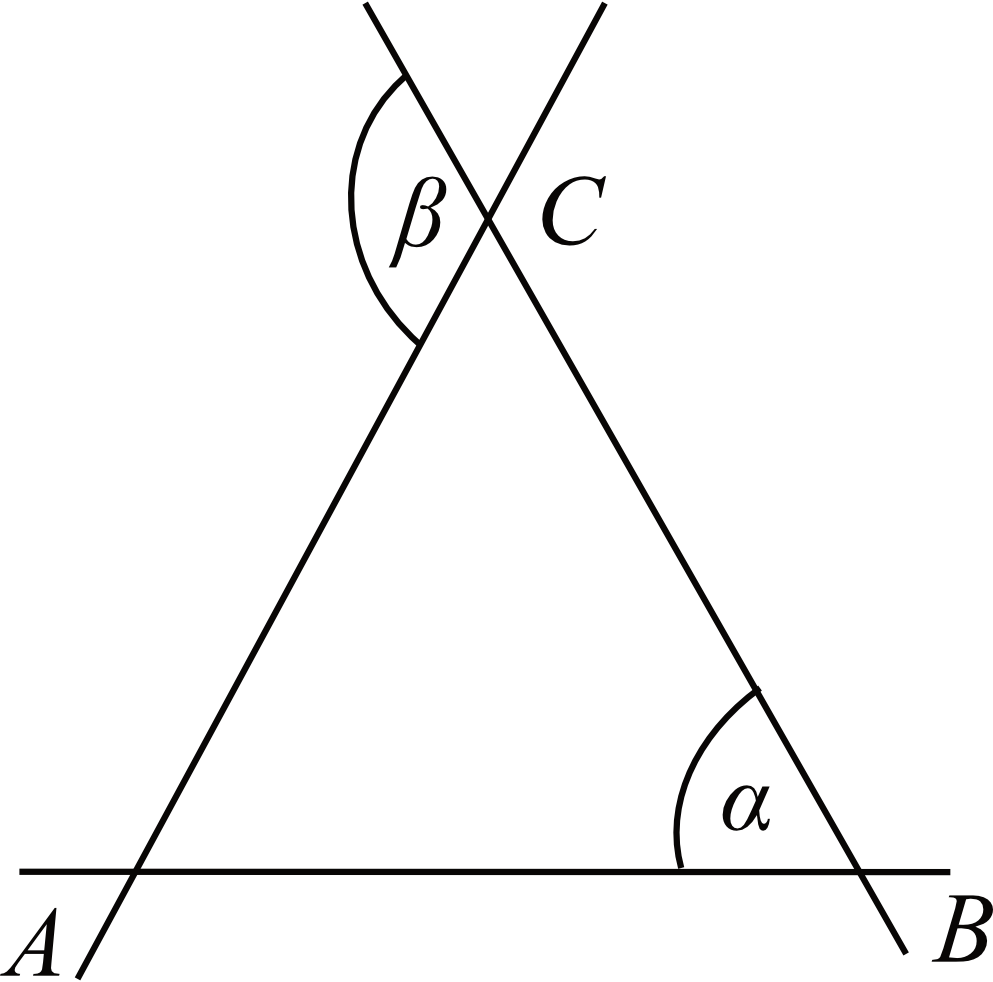
Trzy proste przecinają się w punktach \(A\), \(B\) i \(C\) tak, jak pokazano na rysunku. Odcinki \(AC\) i \(BC\) są równej długości. Wykaż, że miara kąta \(α\) stanowi połowę miary kąta \(β\).

Odpowiedź:      

Udowodniono, korzystając z własności trójkątów równoramiennych oraz kątów przyległych.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Jeżeli odcinki \(AC\) i \(BC\) są równej długości, to trójkąt \(ABC\) jest równoramienny. W trójkątach równoramiennych kąty przy podstawie mają jednakową miarę, więc \(|\sphericalangle CAB|=\alpha\). Dodatkowo oznaczmy sobie kąt \(ACB\) jako \(\gamma\) i mamy taką oto sytuację: Krok 2. Zakończenie dowodzenia. Skoro suma miar kątów w trójkącie \(ACB\) jest równa \(180°\), a kąty przy podstawie mają miarę \(\alpha\), to: $$2\alpha+\gamma=180°$$ Do miary kąta \(ACB\) możemy też podejść z innej perspektywy. Kąt \(\beta\) oraz kąt \(ACB\) są kątami przyległymi. To prowadzi nas do wniosku, że: $$\beta+\gamma=180°$$ Porównując teraz otrzymane dwa zapisy wyjdzie nam, że: $$2\alpha+\gamma=\beta+\gamma \           ,\ 2\alpha=\beta \           ,\ \alpha=\frac{1}{2}\beta$$ W ten sposób udało nam się wykazać, że kąt \(\alpha\) stanowi połowę miary kąta \(\beta\).

Teoria:      
W trakcie opracowania