Na rysunku pokazano plan dwóch dróg, którymi Ula chodzi do szkoły.





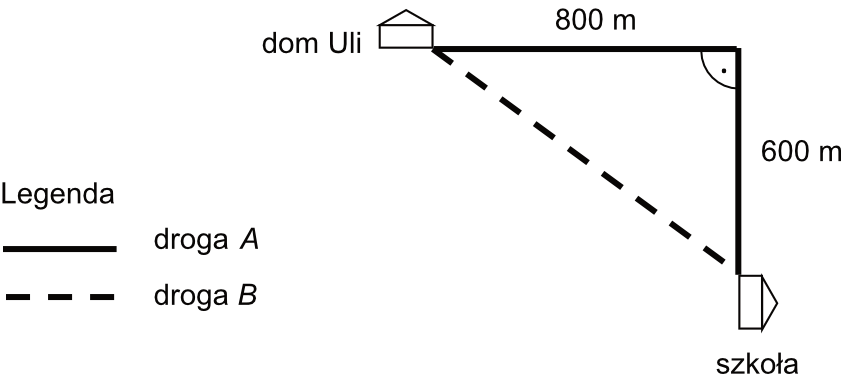
Przyjmij, że Ula porusza się ze stałą prędkością \(4\frac{km}{h}\). Oblicz, o ile minut krócej Ula idzie do szkoły drogą \(B\) niż drogą \(A\). Zapisz obliczenia.

Odpowiedź:      

Ula idzie do szkoły drogą \(B\) o \(6\) minut krócej.

Rozwiązanie:      
Krok 1. Obliczenie długości drogi \(B\). Zacznijmy od obliczenia długości drogi \(B\) (czyli tej po ukosie). Z racji tego, iż na rysunku mamy trójkąt prostokątny, to możemy skorzystać z Twierdzenia Pitagorasa: $$600^2+800^2=c^2 \           ,\ 360000+640000=c^2 \           ,\ c^2=1000000 \           ,\ c=1000$$ Wyszło nam, że długość drogi \(B\) jest równa \(1000m\), czyli \(1km\). Zamiana metrów na kilometry jest bardzo ważna, ponieważ prędkość mamy wyrażoną w \(\frac{km}{h}\). Krok 2. Obliczenie czasu pokonania drogi \(A\). Droga \(A\) ma długość \(800m+600m=1400m=1,4km\). Wiemy, że Ula porusza się z prędkością \(4\frac{km}{h}\), zatem korzystając ze wzoru na prędkość \(v=\frac{s}{t}\) możemy zapisać, że: $$v=\frac{s}{t} \           ,\ vt=s \           ,\ t=\frac{s}{v}$$ Podstawiając teraz dane \(s=1,4km\) oraz \(v=4\frac{km}{h}\), otrzymamy: $$t=\frac{1,4km}{4\frac{km}{h}} \           ,\ t=0,35h$$ Krok 3. Obliczenie czasu pokonania drogi \(B\). Analogicznie obliczymy czas pokonania drogi \(B\). Tutaj \(s=1km\) oraz \(v=4\frac{km}{h}\), zatem: $$t=\frac{s}{v} \           ,\ t=\frac{1km}{4\frac{km}{h}} \           ,\ t=0,25h$$ Krok 4. Obliczenie różnicy czasu. Skoro drogę \(A\) pokonujemy w czasie \(0,35h\), a drogę \(B\) w czasie \(0,25h\), to różnica czasu wyniesie: $$0,35h-0,25h=0,1h$$ Proszą nas o podanie tego czasu w minutach, a skoro jedna godzina to \(60\) minut, to: $$0,1\cdot60min.=6min.$$ To oznacza, że Ula idzie do szkoły drogą \(B\) o \(6\) minut krócej.

Teoria:      
W trakcie opracowania