Prostokąt \(ABCD\) o wymiarach \(7\) cm i \(8\) cm rozcięto wzdłuż prostej \(a\) na dwa trapezy tak, jak pokazano na rysunku. Odcinek \(CL\) ma długość \(3,2cm\).





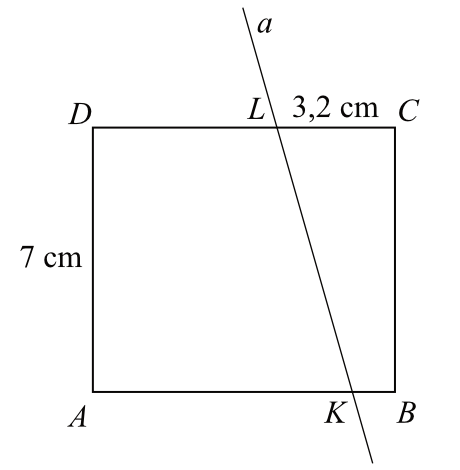
Pole trapezu \(KBCL\) jest czterokrotnie mniejsze od pola prostokąta \(ABCD\). Oblicz długość odcinka \(KB\). Zapisz obliczenia.

Odpowiedź:      

\(|KB|=0,8cm\)

Rozwiązanie:      
Krok 1. Obliczenie pola powierzchni trapezu \(KBCL\). Z treści zadania wynika, że prostokąt \(ABCD\) ma wymiary \(7cm\times8cm\). W związku z tym pole tego prostokąta jest równe: $$P_{ABCD}=7cm\cdot8cm=56cm^2$$ Jeżeli pole trapezu jest czterokrotnie mniejsze od pola tego prostokąta, to znaczy że to pole jest równe: $$P_{KBCL}=56cm^2:4=14cm^2$$ Krok 2. Obliczenie długości odcinka \(KB\). O trapezie \(KBCL\) wiemy, że jedna z jego podstaw ma długość \(a=3,2cm\), wysokość ma miarę \(h=7cm\), a pole tego trapezu jest równe \(P=14cm^2\). W związku z tym jeżeli podstawę \(KB\) oznaczymy sobie symbolem \(b\), to korzystając ze wzoru na pole trapezu możemy zapisać, że: $$P=\frac{a+b}{2}\cdot h \           ,\ 14cm^2=\frac{3,2cm+b}{2}\cdot7cm \quad\bigg/:7cm \           ,\ 2cm^2=\frac{3,2cm+b}{2} \quad\bigg/\cdot2 \           ,\ 4cm^2=3,2cm+b \           ,\ b=0,8cm$$ To oznacza, że odcinek \(KB\) ma miarę \(0,8cm\).

Teoria:      
W trakcie opracowania