W trójkącie \(KLM\) poprowadzono wysokość \(KN\). Długości niektórych odcinków opisano za pomocą wyrażeń algebraicznych: \(|KL|=2y\), \(|LM|=2x\), \(|KN|=k+1\).





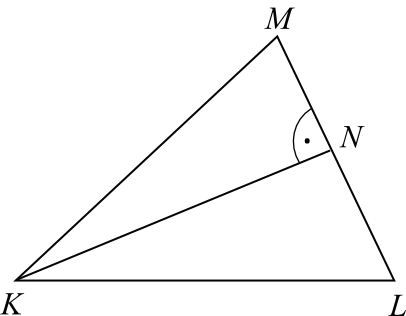
Pole trójkąta \(KLM\) opisano wyrażeniem:

A \(x(k+1)\)
B \(2x(k+1)\)
C \(y(k+1)\)
D \(2y(k+1)\)

Odpowiedź:      

A

Rozwiązanie:      
W tym zadaniu musimy zwrócić uwagę na to, że wysokość \(KN\) pada na bok \(LM\), zatem to bok \(LM\) jest naszą podstawą trójkąta. Korzystając ze wzoru na pole trójkąta możemy zapisać, że: $$P=\frac{1}{2}a\cdot h \           ,\ P=\frac{1}{2}\cdot|LM|\cdot|KN|$$ Z treści zadania wiemy, że \(|LM|=2x\) oraz że \(|KN|=k+1\), zatem: $$P=\frac{1}{2}\cdot2x\cdot(k+1) \           ,\ P=x\cdot(k+1)$$

Teoria:      
W trakcie opracowania