Zbiory arkuszy egzaminacyjnych z matematyki dla ósmoklasistów. Znajdziesz tu różnorodne zadania egzaminacyjne, przykładowe arkusze, rozwiązania zadań, testy z matematyki oraz wiele innych przydatnych materiałów
Próbny egzamin ósmoklasisty z matematyki - Operon 2021 Zadanie 14 z 19
Zadanie nr 14. (1pkt)
Na boku kwadratu \(ABCD\) zbudowano trójkąt równoboczny \(BEC\), jak na rysunku.
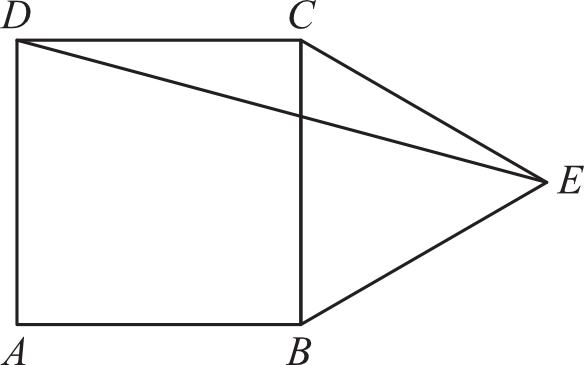
Kąt \(CDE\) ma miarę:
A \(15°\)
B \(22,5°\)
C \(30°\)
D \(45°\)
Rozwiązanie:
Krok 1. Obliczenie miary kąta \(DCE\).
Kąt DCE składa się z kąta prostego oraz kąta \(BCE\). Jeżeli trójkąt \(BEC\) jest równoboczny, to kąt \(BCE\) jest kątem o mierze \(60°\). To oznacza, że:
$$|\sphericalangle DCE|=90°+60°=150°$$
Krok 2. Obliczenie miary kąta \(CDE\).
Trójkąt \(DEC) jest trójkątem równoramiennym (boki \(DC) oraz \(CE) mają jednakową długość, ponieważ bok kwadratu i trójkąta ma tą samą miarę). Z własności takich trójkątów wynika, że kąty przy podstawie mają jednakową miarę. Skoro kąt między ramionami ma \(150°\), to na kąty przy podstawie zostaje nam \(180°-150°=30°\). Tym samym kąt \(CDE\) będzie miał miarę:
$$|\sphericalangle CDE|=30°:2=15°$$
Teoria:
W trakcie opracowania
Operon

