Dany jest trójkąt \(ABC\), w którym \(|BC|=6\). Miara kąta \(ACB\) jest równa \(150°\) (zobacz rysunek).





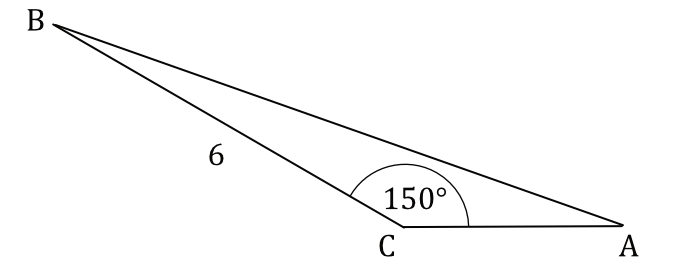
Wysokość trójkąta \(ABC\) opuszczona z wierzchołka \(B\) jest równa:

A \(3\)
B \(4\)
C \(3\sqrt{3}\)
D \(4\sqrt{3}\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Gdy poprowadzimy wysokość trójkąta z wierzchołka \(B\) to powstanie nam taka oto sytuacja: Krok 2. Obliczenie wysokości trójkąta. Powstał nam trójkąt prostokątny \(DBC\) i jest to trójkąt o kątach \(30°, 60°, 90°\). Z własności takich trójkątów wynika, że nasza krótsza przyprostokątna (która jest jednocześnie wysokością trójkąta) będzie dwa razy krótsza od przeciwprostokątnej, zatem: $$h=6:2 \           ,\ h=3$$ Do tego samego wyniku dojdziemy oczywiście korzystając z funkcji trygonometrycznych. W tym przypadku pomoże nam sinus, zatem: $$sin30°=\frac{h}{6} \           ,\ \frac{1}{2}=\frac{h}{6} \           ,\ h=3$$

Teoria:      
W trakcie opracowania