Dany jest sześcian \(ABCDEFGH\). Odcinek łączący wierzchołek \(H\) ze środkiem krawędzi \(BC\) ma długość \(HP=4\) (jak na rysunku).





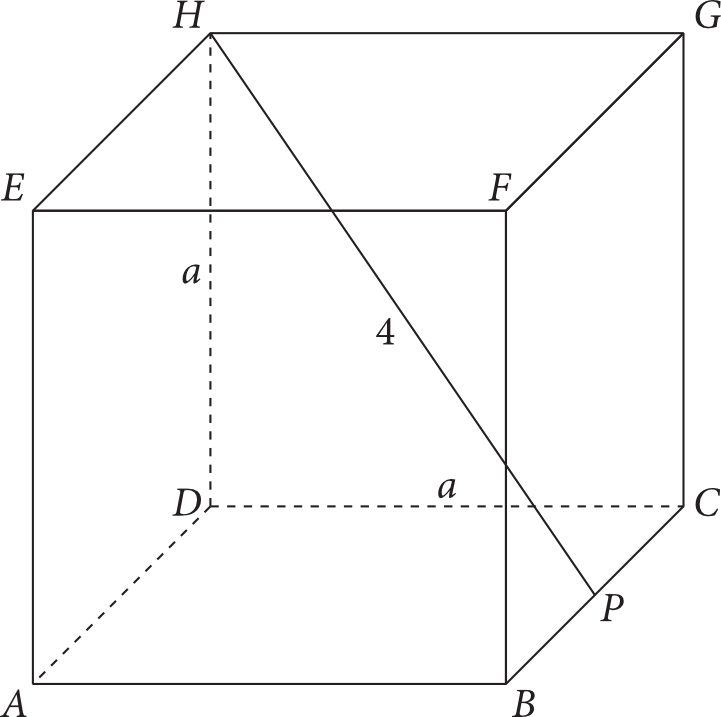
Oblicz objętość tego sześcianu.

Odpowiedź:      

\(V=18\frac{26}{27}\)

Rozwiązanie:      
Krok 1. Obliczenie długości krawędzi sześcianu. Kluczem do sukcesu jest dostrzeżenie, iż trójkąt \(PCH\) jest prostokątny. Skoro tak, to pomoże nam tutaj Twierdzenie Pitagorasa. Jeżeli przyjmiemy, że długość krawędzi sześcianu ma długość \(a\), to \(|PC|=\frac{1}{2}a\) natomiast \(|CH|=a\sqrt{2}\) (bo jest to przekątna kwadratu o boku \(a\)). W treści zadania mamy jeszcze podaną długość \(|HP|=4\) (która jest przeciwprostokątną naszego trójkąta), zatem: $$\left(\frac{1}{2}a\right)^2+(a\sqrt{2})^2=4^2 \           ,\ \frac{1}{4}a^2+2a^2=16 \           ,\ \frac{9}{4}a^2=16 \quad\bigg/\cdot\frac{4}{9} \           ,\ a^2=\frac{64}{9} \           ,\ a=\sqrt{\frac{64}{9}} \quad\lor\quad a=-\sqrt{\frac{64}{9}} \           ,\ a=\frac{8}{3} \quad\lor\quad a=-\frac{8}{3}$$ Krok 2. Obliczenie objętości sześcianu. $$V=a^3 \           ,\ V=\left(\frac{8}{3}\right)^3 \           ,\ V=\frac{512}{27}=18\frac{26}{27}$$

Teoria:      
W trakcie opracowania