Na okręgu o środku \(S\) leżą punkty \(A\), \(B\), \(C\) i \(D\). Odcinek \(AB\) jest średnicą tego okręgu. Kąt między tą średnicą a cięciwą \(AC\) jest równy \(21°\) (zobacz rysunek).







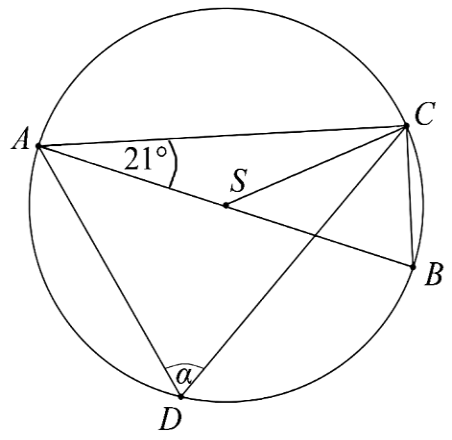
Kąt \(α\) między cięciwami \(AD\) i \(CD\) jest równy:

A \(21°\)
B \(42°\)
C \(48°\)
D \(69°\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(ASC\). Musimy zauważyć, że trójkąt \(ACS\) jest trójkątem równoramiennym. Skąd to wiemy? Jego ramiona \(AS\) oraz \(CS\) mają długość równą długości promienia tego okręgu. Skoro tak, to kąty przy podstawie \(AC\) mają równą miarę, a to pozwoli nam wyznaczyć miarę kąta \(ASC\): $$|\sphericalangle ASC|=180°-21°-21° \           ,\ |\sphericalangle ASC|=138°$$ Krok 2. Obliczenie miary kąta \(ADC\). Kąt wpisany jest dwa razy mniejszy od miary kąta środkowego opartego na tym samym łuku. Zatem: $$|\sphericalangle ASC|=138°:2 \           ,\ |\sphericalangle ASC|=69°$$

Teoria:      
W trakcie opracowania