W układzie współrzędnych narysowano część paraboli o wierzchołku w punkcie \(A=(2,4)\), która jest wykresem funkcji kwadratowej \(f\).







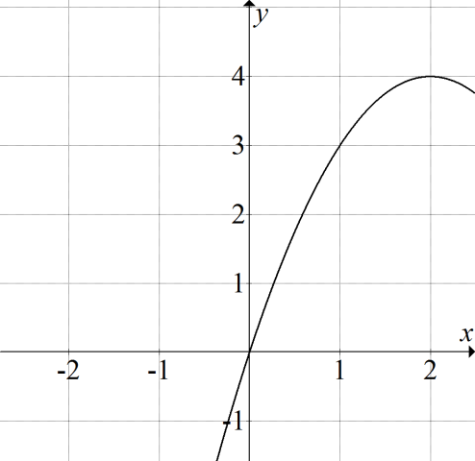
Funkcja \(f\) może być opisana wzorem:

A \(f(x)=(x-2)^2+4\)
B \(f(x)=(x+2)^2+4\)
C \(f(x)=-(x-2)^2+4\)
D \(f(x)=-(x+2)^2+4\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Odczytanie informacji z wykresu. Z wykresu funkcji kwadratowej musimy odczytać dwie kluczowe informacje: - współrzędne wierzchołka \(W=(2;4)\). - współczynnik kierunkowy \(a\) - ramiona są skierowane do dołu, więc na pewno \(a\lt0\). Krok 2. Ustalenie wzoru funkcji kwadratowej. Funkcja kwadratowa o wierzchołku w punkcie \(W=(p;q)\) przyjmuje wzór: $$y=a(x-p)^2+q$$ W naszym przypadku będzie to w takim razie: $$y=a(x-2)^2+4$$ Pasują nam w tym momencie dwie odpowiedzi: \(A\) oraz \(C\). Z racji tego, że ramiona paraboli są skierowane do dołu i współczynnik kierunkowy \(a\lt0\), to prawidłową odpowiedzią będzie \(C\), gdyż to właśnie tam na początku znalazł się minus.

Teoria:      
W trakcie opracowania