Na przekątnej \(BD\) kwadratu \(ABCD\) o boku długości \(4\) zbudowano trójkąt równoboczny \(BED\).





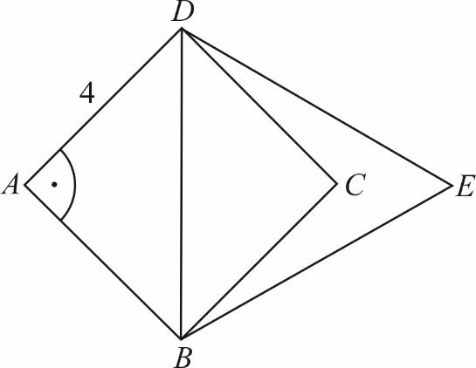
Pole trójkąta \(BED\) jest równe:

A \(2\sqrt{6}\)
B \(4\sqrt{6}\)
C \(8\sqrt{3}\)
D \(16\sqrt{3}\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Obliczenie długości boku trójkąta. Bok trójkąta jest jednocześnie długością przekątnej \(DB\). Przekątna kwadratu o boku \(a=4\) ma długość \(a\sqrt{2}\), zatem: $$DB=4\sqrt{2}$$ Krok 2. Obliczenie pola trójkąta równobocznego. Znając długość boku możemy bez problemu obliczyć pole trójkąta równobocznego, korzystając z następującego wzoru: $$P=\frac{a^2\sqrt{3}}{4} \           ,\ P=\frac{(4\sqrt{2})^2\cdot\sqrt{3}}{4} \           ,\ P=\frac{16\cdot2\cdot\sqrt{3}}{4} \           ,\ P=\frac{32\sqrt{3}}{4} \           ,\ P=8\sqrt{3}$$

Teoria:      
W trakcie opracowania