Na kwadratowej siatce narysowano pewien wielokąt (patrz rysunek). Jego wierzchołki znajdują się w punktach przecięcia linii siatki.





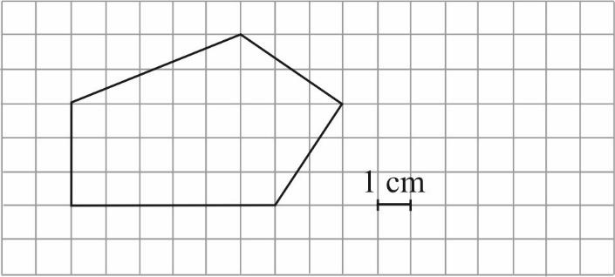
Pole tego wielokąta jest równe:

A \(18cm^2\)
B \(21cm^2\)
C \(29cm^2\)
D \(32cm^2\)

Odpowiedź:      

C

Rozwiązanie:      
Krok 1. Podzielenie figury na mniejsze części. Aby rozwiązać to zadanie musimy podzielić ten wielokąt na dwie różne figury, których pola będziemy w stanie obliczyć. Jedną z figur będzie trójkąt o podstawie długości \(8cm\) i wysokości \(2cm\). Drugą figurą będzie trapez o podstawach \(6cm\) i \(8cm\) oraz wysokości \(3cm\). Krok 2. Obliczenie pola powierzchni trójkąta. $$P_{1}=\frac{1}{2}ah \           ,\ P_{1}=\frac{1}{2}\cdot8\cdot2 \           ,\ P_{1}=8[cm^2]$$ Krok 3. Obliczenie pola powierzchni trapezu. $$P_{2}=\frac{1}{2}(a+b)\cdot h \           ,\ P_{2}=\frac{1}{2}\cdot(6+8)\cdot3 \           ,\ P_{2}=\frac{1}{2}\cdot14\cdot3 \           ,\ P_{2}=7\cdot3 \           ,\ P_{2}=21$$ Krok 4. Obliczenie pola powierzchni figury. Cała figura jest sumą pól powierzchni trójkąta i trapezu, zatem jej pole będzie równe: $$P=P_{1}+P_{2} \           ,\ P=8cm^2+21cm^2 \           ,\ P=29cm^2$$

Teoria:      
W trakcie opracowania