Na rysunku przedstawiono okrąg o środku \(O\) oraz kąt środkowy o mierze \(280°\). Punkty \(A\) i \(B\) znajdują się na okręgu. Prosta \(k\) jest styczna do okręgu w punkcie \(B\).







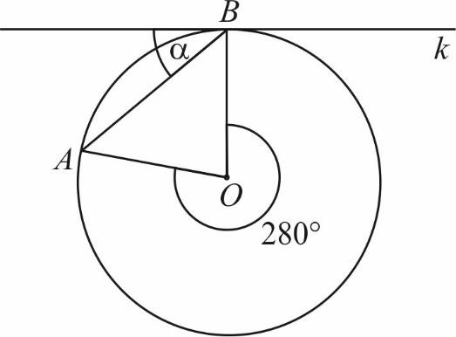
Miara kąta \(α\) jest równa:

A 30°
B 40°
C 50°
D 80°

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Wyznaczenie miary kąta \(AOB\). Kąt \(AOB\) będzie miał miarę: $$|\sphericalangle AOB|=360°-280°=80°$$ Krok 2. Wyznaczenie miar kąta \(ABO\). Trójkąt \(AOB\) jest na pewno równoramienny. Skąd to wiemy? Jego boki \(AO\) oraz \(BO\) mają długość promienia okręgu. To z kolei oznacza, że kąty przy podstawie \(AB\) muszą mieć jednakową miarę. Skoro suma kątów w trójkącie jest równa \(180°\), a \(|\sphericalangle AOB|=80°\), to znaczy, że: $$|\sphericalangle ABO|=(180°-80°):2=100°:2=50°$$ Krok 3. Wyznaczenie miary kąta \(α\). Styczna do okręgu jest jednocześnie prostopadła do promienia (to jedna z ważniejszych własności stycznych w okręgach). Skoro tak, to nasz kąt \(α\) będzie mieć miarę: $$α=90°-50°=40°$$

Teoria:      
W trakcie opracowania