Ciocia Jola uszyła serwetę ze skośnymi brzegami, która pasuje do prostokątnego stolika o wymiarach \(100cm\) i \(40cm\) (jak na rysunku).





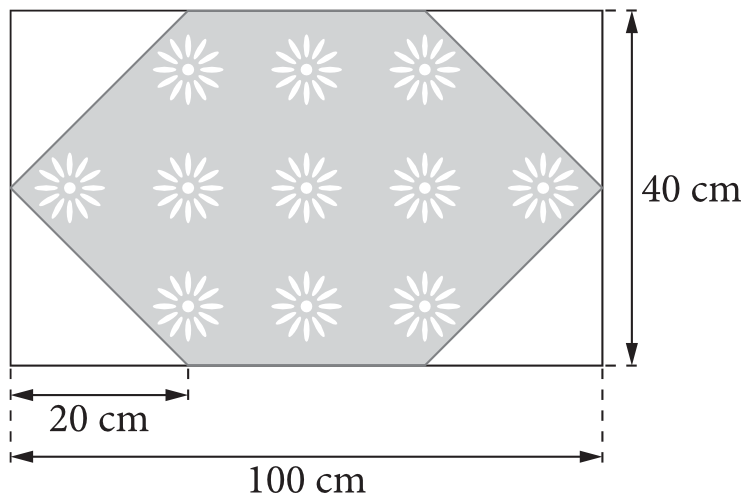
Brzeg serwety chce obszyć kolorową tasiemką. Czy na obszycie wystarczy \(2,5m\) tasiemki? Przyjmij \(\sqrt{2}\approx1,4\).

Odpowiedź:      

Tasiemka o długości \(2,5m\) jest wystarczająca.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Powinniśmy zauważyć, że w rogach rysunku mamy trójkąty prostokątne, których przyprostokątne mają długość \(20cm\). Wspominamy sobie o tych trójkątach, bowiem na obwód serwety składają się m.in. przeciwprostokątne tychże trójkątów (oznaczymy je sobie na szkicu jako \(x\)). Dodatkowo na dole i górze mamy fragmenty serwetki, które oznaczymy sobie jako \(y\). Całość na rysunku z oznaczeniami będzie wyglądać następująco: Krok 2. Obliczenie długości odcinków oznaczonych jako \(x\). Na rysunku mamy cztery odcinki oznaczone jako \(x\), zatem obliczmy miarę każdego z takich boków. Możemy skorzystać tutaj wprost z Twierdzenia Pitagorasa i zapisać, że \(20^2+20^2=x^2\), ale możemy też postąpić nieco sprytniej. Tak naprawdę nasze trójkąty prostokątne są klasycznymi trójkątami o kątach \(45°, 45°, 90°\) (wiemy to, bo przyprostokątne mają jednakową długość). Z własności takich trójkątów wynika, że ich przeciwprostokątna jest \(\sqrt{2}\) razy dłuższa od długości przyprostokątnych, zatem możemy zapisać od razu, że \(x=20\sqrt{2}cm\). Krok 3. Obliczenie długości odcinków oznaczonych jako \(y\). Odcinki oznaczone jako \(y\) są dość proste do policzenia, bowiem będzie to długość \(100cm\), która jest pomniejszona z lewej i prawej strony o \(20cm\). Możemy więc zapisać, że: $$y=100cm-2\cdot20cm \           ,\ y=100cm-40cm \           ,\ y=60cm$$ Krok 4. Obliczenie obwodu całej serwety. Na obwód naszej serwety składają się cztery odcinki oznaczone jako \(x\) oraz dwa odcinki oznaczone jako \(y\), zatem: $$Obw=4\cdot20\cdot{2}+2\cdot60 \           ,\ Obw=80\sqrt{2}+120[cm]$$ Przyjmując przybliżenie \(\sqrt{2}\approx1,4\) otrzymamy: $$Obw\approx80\cdot1,4+120 \           ,\ Obw\approx112+120 \           ,\ Obw\approx232[cm]\approx2,32m$$ To oznacza, że tasiemka o długości \(2,5m\) jak najbardziej wystarczy do obszycia naszej serwety.

Teoria:      
W trakcie opracowania