W trójkącie równoramiennym \(ABC\), w którym \(|AC|=|BC|\), poprowadzono dwie wysokości: \(AD\) i \(CE\). Na rysunku przedstawiono ten trójkąt i zaznaczono w nim niektóre kąty.





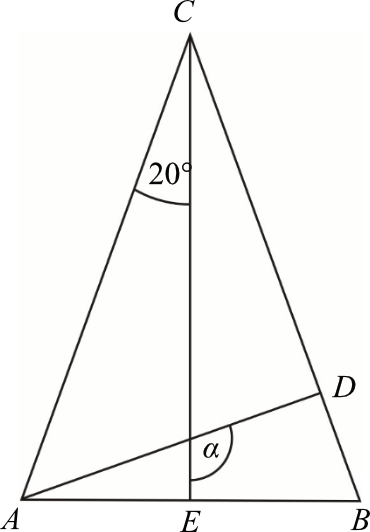
Uzasadnij, że kąt \(\alpha\) ma miarę \(110°\).

Odpowiedź:      

Uzasadniono, korzystając z własności trójkątów równoramiennych oraz kątów przyległych.

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Zaznaczmy na rysunku kąty proste oraz oznaczmy miejsce przecięcia się wysokości jako punkt \(S\): Krok 2. Obliczenie miary kąta \(ECB\) oraz \(CSD\). Trójkąt \(ABC\) jest równoramienny, zatem wysokość \(CE\) dzieli nam kąt \(ACB\) na dwie równe części. To prowadzi nas do wniosku, że kąt \(ECB\) ma także miarę \(20°\). Spójrzmy teraz na trójkąt \(SDC\). Znamy już dwie miary kątów w tym trójkącie, zatem kąt \(CSD\) będzie mieć miarę: $$180°-90°-20°=70°$$ Krok 3. Obliczenie miary kąta \(\alpha\). Kąty \(CSD\) oraz poszukiwany kąt \(\alpha\) to kąty przyległe, zatem łączna miara tych dwóch kątów jest równa \(180°\). Skoro tak, to: $$\alpha=180°-70°=110°$$

Teoria:      
W trakcie opracowania