Na rysunku przedstawiono dwa trójkąty oraz podano niektóre ich wymiary i miary kilku kątów.





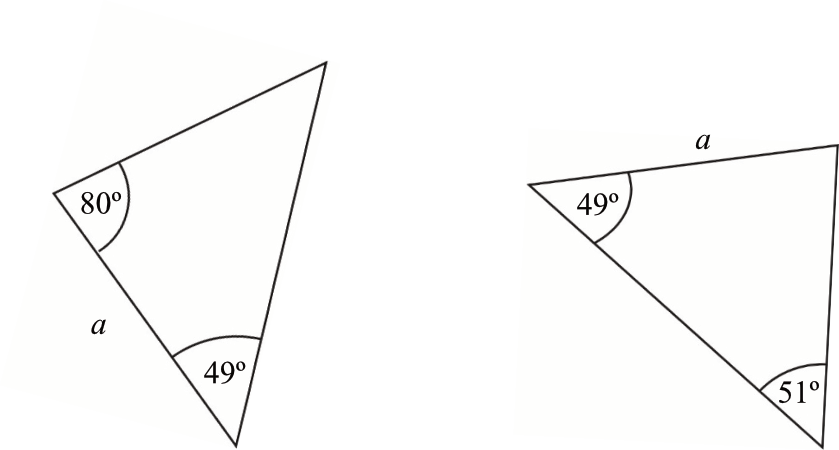
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, albo F – jeśli jest fałszywe. Te trójkąty są równoramienne.
Te trójkąty są przystające.

Te trójkąty są równoramienne.

Odpowiedź:      

1) FAŁSZ

2) PRAWDA

Rozwiązanie:      
Krok 1. Wyznaczenie miar kątów w trójkątach. Znamy dwie miary kątów w każdym z trójkątów. Policzmy zatem miary brakujących kątów: Pierwszy trójkąt: $$180°-80°-49°=51°$$ Drugi trójkąt: $$180°-51°-49°=80°$$ To oznacza, że obydwa trójkąty mają kąty o miarach \(49°, 51°, 80°\). Krok 2. Ocena prawdziwości pierwszego zdania. W trójkątach równoramiennych mamy parę kątów o jednakowej mierze (kąty przy podstawie mają tą samą miarę). W przypadku podanych trójkątów takiej sytuacji nie mamy (każdy kąt ma inną miarę), więc na pewno nie będą to trójkąty równoramienne. Zdanie jest więc fałszem. Krok 3. Ocena prawdziwości drugiego zdania. Wiemy już, że obydwa trójkąty mają jednakowe miary kątów: \(49°, 51°, 80°\). To oznacza, że na pewno są to trójkąty podobne (cecha kąt-kąt-kąt), ale nie wiemy jeszcze, czy są przystające (czyli czy oprócz jednakowych kątów, mają one jeszcze jednakowe długości boków). Spójrzmy na zaznaczone odcinki \(a\). Zarówno w jednym, jak i drugim trójkącie, odcinek \(a\) jest przy kątach o mierze \(49°\) oraz \(80°\). To pozwala nam stwierdzić, że te trójkąty są faktycznie przystające (cecha kąt-bok-kąt). Zdanie jest więc prawdą.

Teoria:      
W trakcie opracowania