Zbiory arkuszy egzaminacyjnych z matematyki dla ósmoklasistów. Znajdziesz tu różnorodne zadania egzaminacyjne, przykładowe arkusze, rozwiązania zadań, testy z matematyki oraz wiele innych przydatnych materiałów
Egzamin ósmoklasisty (termin dodatkowy) 2019 - matematyka Zadanie 10 z 21
Zadanie nr 10. (1pkt)
W prostokątnym układzie współrzędnych zaznaczono wierzchołki trójkąta prostokątnego \(ABC\) (patrz: rysunek).
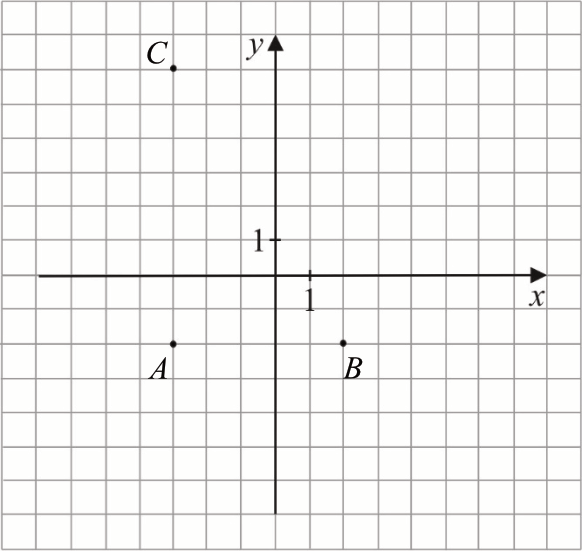
Przeciwprostokątna trójkąta \(ABC\) ma długość:
A \(\sqrt{39}\)
B \(10\)
C \(\sqrt{89}\)
D \(13\)
Rozwiązanie:
Odcinek \(AB\) ma \(5\) jednostek (\(5\) kratek), natomiast odcinek \(AC\) ma długość \(8\) jednostek. Korzystając z Twierdzenia Pitagorasa możemy więc zapisać, że:
$$5^2+8^2=|AC|^2 \ ,\
25+64=|AC|^2 \ ,\
|AC|^2=89 \ ,\
|AC|=\sqrt{89} \quad\lor\quad |AC|=-\sqrt{89}$$
Długość boku musi być dodatnia, zatem zostaje nam \(|AC|=\sqrt{89}\).
Teoria:
W trakcie opracowania
CKE

