Duży prostokąt przedstawiony na rysunku jest podzielony na osiem małych przystających prostokątów.





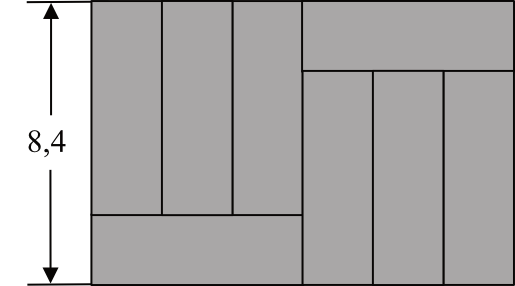
Oblicz obwód dużego prostokąta. Zapisz obliczenia.

Odpowiedź:      

\(Obw=42\)

Rozwiązanie:      
Krok 1. Sporządzenie rysunku pomocniczego. Małe prostokąty są przystające, czyli mówiąc wprost - każdy z nich ma te same wymiary. Kluczem do sukcesu jest dostrzeżenie, że dłuższy bok prostokąta ma miarę trzy razy większą od krótszego boku: Krok 2. Obliczenie długości krótszego boku prostokąta. Z rysunku wynika, że suma dłuższego i krótszego boku prostokąta ma łącznie długość \(8,4\). Stosując zatem nasze oznaczenia, możemy zapisać, że: $$3x+x=8,4 \           ,\ 4x=8,4 \           ,\ x=2,1$$ To oznacza, że krótszy bok prostokąta ma długość \(2,1\). Gdyby zaszła taka potrzeba, moglibyśmy przy okazji policzyć, że dłuższy bok prostokąta ma długość \(3\cdot2,1=6,3\). Krok 3. Obliczenie obwodu dużego prostokąta. Celem zadania jest obliczenie obwodu dużego prostokąta. Patrząc się na rysunek widzimy, że dolny bok prostokąta ma długość \(3x+x+x+x=6x\), a boczny bok ma długość \(3x+x=4x\) (lub po prostu \(8,4\), bo wynika to z rysunku). To oznacza, że obwód tej figury jest równy: $$Obw=2\cdot6x+2\cdot4x \           ,\ Obw=12x+8x \           ,\ Obw=20x \           ,\ Obw=20\cdot2,1 \           ,\ Obw=42$$

Teoria:      
W trakcie opracowania