Prostokątna łąka jest podzielona na dwie części \(A\) i \(B\), tak jak pokazano na rysunku. Każda z tych części ma kształt trapezu.





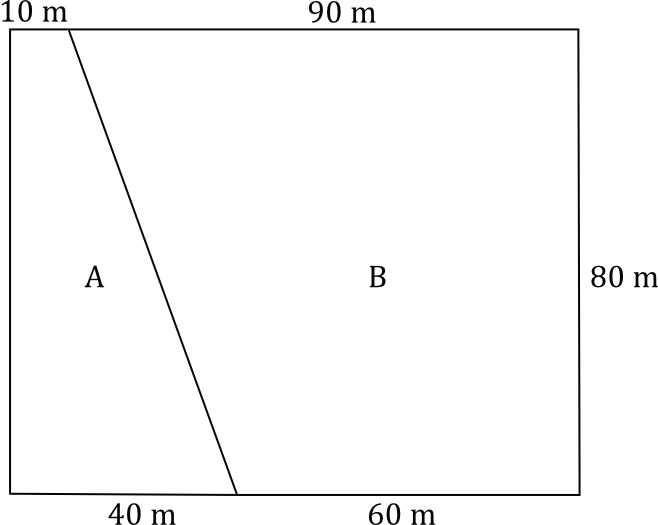
Kosiarka w ciągu każdej godziny swojej pracy kosi trawę z powierzchni o takim samym polu. Trawę z części \(A\) kosiarka skosiła w ciągu trzech godzin. Oblicz, ile godzin kosiarka będzie kosiła trawę w części \(B\). Zapisz obliczenia.

Odpowiedź:      

\(9\) godzin

Rozwiązanie:      
Krok 1. Obliczenie pola powierzchni części \(A\). Korzystając ze wzoru na pole trapezu, możemy zapisać, że pole części \(A\) będzie równe: $$P=\frac{1}{2}(a+b)\cdot h \           ,\ P=\frac{1}{2}(40m+10m)\cdot80m \           ,\ P=\frac{1}{2}\cdot50m\cdot80m \           ,\ P=25m\cdot80m \           ,\ P=2000m^2$$ Krok 2. Obliczenie pola powierzchni części \(B\). Korzystając ze wzoru na pole trapezu, możemy zapisać, że pole części \(B\) będzie równe: $$P=\frac{1}{2}(a+b)\cdot h \           ,\ P=\frac{1}{2}(60m+90m)\cdot80m \           ,\ P=\frac{1}{2}\cdot150m\cdot80m \           ,\ P=75m\cdot80m \           ,\ P=6000m^2$$ Krok 3. Obliczenie czasu koszenia części \(B\). Pole powierzchni części \(B\) jest \(3\) razy większe od pola \(A\), ponieważ \(6000m^2:2000m^2=3\). To oznacza, że tym samym czas koszenia będzie trzykrotnie dłuższy. Możemy więc powiedzieć, że w części \(B\) kosiarka będzie kosiła przez: $$3\cdot3h=9h$$

Teoria:      
W trakcie opracowania