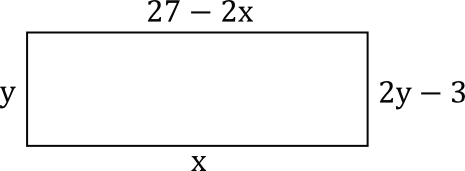Na rysunku przedstawiono prostokąt. Długość dłuższego boku oznaczono symbolem \(x\) oraz opisano za pomocą wyrażenia algebraicznego \(27-2x\). Długość krótszego boku oznaczono symbolem \(y\) oraz opisano za pomocą wyrażenia algebraicznego \(2y-3\).





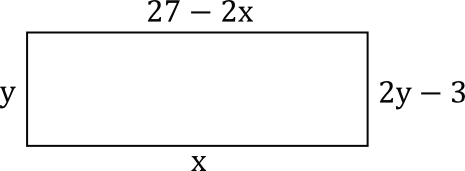
Które równanie nie opisuje poprawnej zależności między wartościami \(x\) i \(y\)?

A \(x-y=6\)
B \(x+y=12\)
C \(x\cdot y=27\)
D \(y:x=3\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie wartości \(x\) oraz \(y\). Leżące naprzeciw siebie długości boków prostokąta mają jednakowe miary. To pozwoli nam ułożyć dwa następujące równania, z których obliczymy wartości \(x\) oraz \(y\). Pierwsza para boków: $$x=27-2x \           ,\ 3x=27 \           ,\ x=9$$ Druga para boków: $$y=2y-3 \           ,\ -y=-3 \           ,\ y=3$$ Krok 2. Sprawdzenie, które z podanych równań jest niepoprawne. Musimy sprawdzić, które z podanych równań jest niepoprawne. W tym celu najłatwiej będzie podstawić wyznaczone \(x=9\) oraz \(y=3\) do działań znajdujących się po lewej stronie równań i sprawdzić, czy otrzymany wynik jest identyczny jak w podanym równaniu. W związku z tym: Odp. A. $$x-y=9-3=6$$ Czyli tutaj opisana zależność \(x-y=6\) jest prawidłowa. Odp. B. $$x+y=9+3=12$$ Czyli tutaj opisana zależność \(x+y=12\) jest prawidłowa. Odp. C. $$x\cdot y=9\cdot3=27$$ Czyli tutaj opisana zależność \(x\cdot y=27\) jest prawidłowa. Odp. D. $$y:x=3:9=\frac{1}{3}$$ Czyli tutaj opisana zależność \(y:x=3\) jest niepoprawna i to właśnie będzie poszukiwana przez nas odpowiedź.

Teoria:      
W trakcie opracowania