Małgosia narysowała równoległobok położony w układzie współrzędnych tak jak na pierwszym rysunku. Kolejne przystające do niego równoległoboki rysowała w taki sposób, że dolny lewy wierzchołek rysowanego równoległoboku był środkiem górnego boku poprzedniego równoległoboku (rysunek 2.).





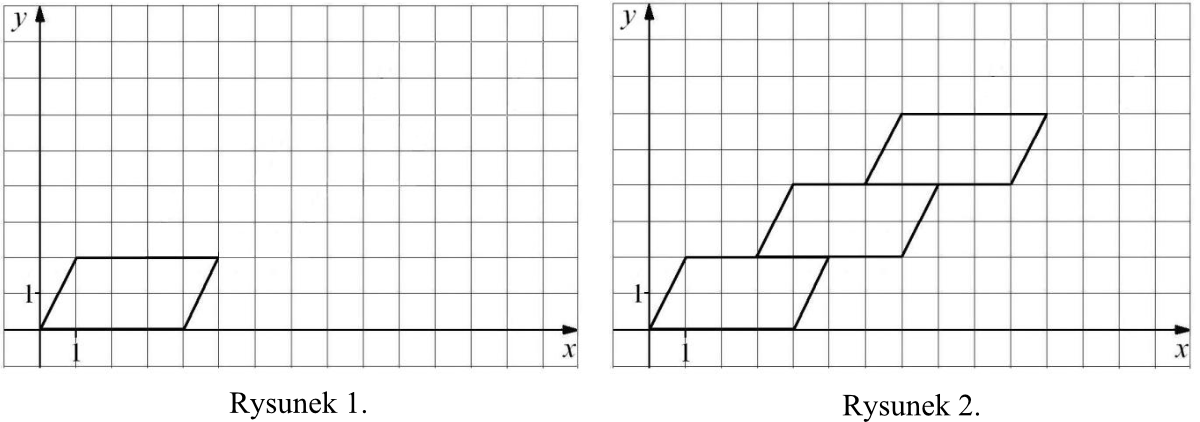
Współrzędne prawego górnego wierzchołka ostatniego narysowanego równoległoboku są równe \((a,b)\). Współrzędne takiego wierzchołka w następnym równoległoboku będą równe:

A \((a+4, b+2)\)
B \((a+2, b+3)\)
C \((a+3, b+2)\)
D \((a+3, b+1)\)

Odpowiedź:      

C

Rozwiązanie:      
Z rysunku wynika, że każdy kolejny równoległobok powiększa współrzędną iksową o \(3\) jednostki, a każdą współrzędną igrekową o \(2\) jednostki. W związku z tym jeżeli współrzędne prawego górnego wierzchołka są równe \((a,b)\), to po dorysowaniu kolejnego równoległoboku będziemy mieć współrzędne \((a+3, b+2)\).

Teoria:      
W trakcie opracowania