Trzy proste przecinające się w sposób przedstawiony na rysunku tworzą trójkąt \(ABC\). Uzasadnij, że trójkąt \(ABC\) jest równoboczny.

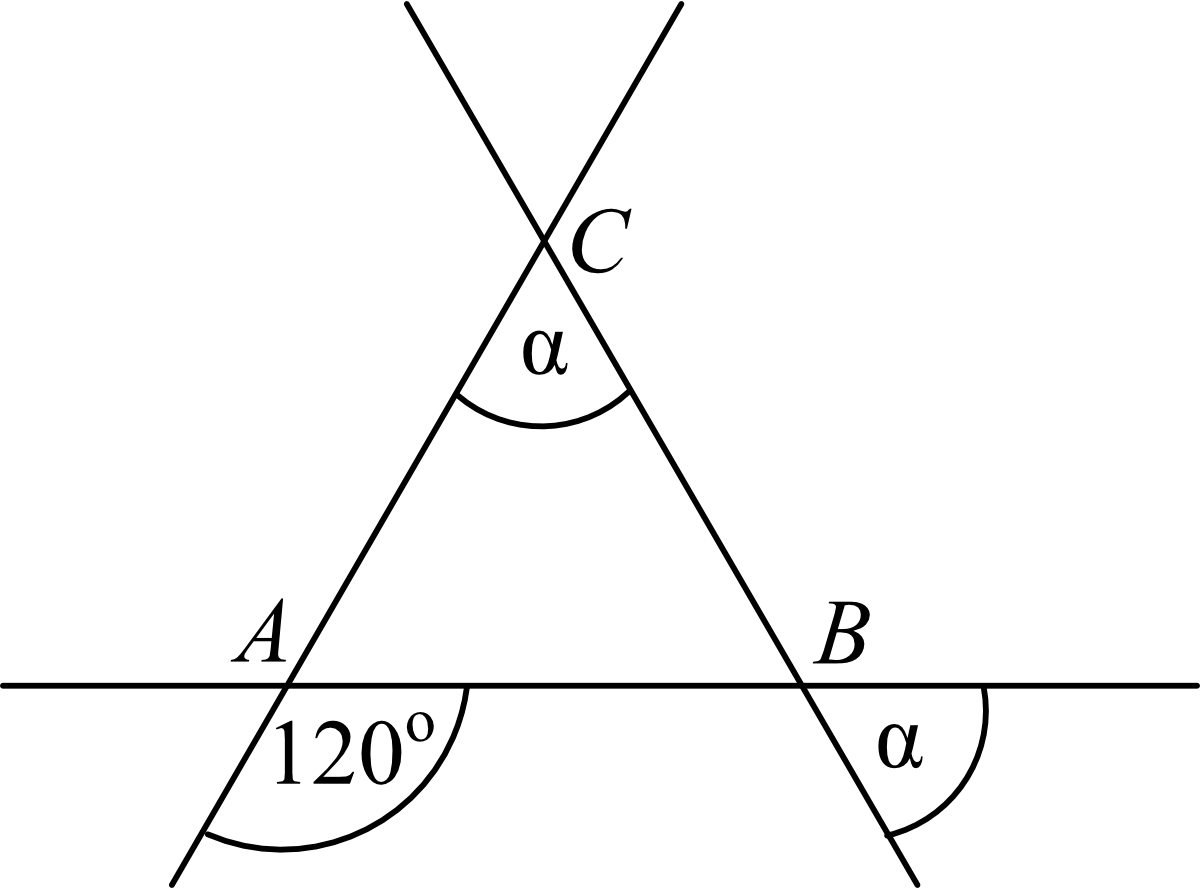
Odpowiedź:      

Udowodniono obliczając miary poszczególnych kątów.

Rozwiązanie:      
Krok 1. Wyznaczenie miary kąta \(CAB\). Kąt \(CAB\) jest kątem przyległym do kąta o mierze \(120°\), a z własności kątów podobnych wiemy, że suma ich miar wynosi \(180°\). To oznacza, że: $$|\sphericalangle CAB|=180°-120°=60°$$ Krok 2. Obliczenie miary kąta \(ABC\) oraz \(ACB\). Zacznijmy od kąta \(ABC\). Jest on kątem wierzchołkowym do kąta \(α\) znajdującego się przy wierzchołku \(B\), zatem możemy zapisać, że: $$|\sphericalangle ABC|=α$$ Mamy więc następującą sytuację: O naszym trójkącie wiemy, że ma w sobie kąt \(60°\) oraz jakieś dwa kąty o jednakowej mierze \(α\). Spróbujmy zatem wyznaczyć wartość tej \(α\). Wiemy, że suma kątów w trójkącie jest równa \(180°\), zatem prawdziwą będzie równość: $$2α+60°=180° \           ,\ 2α=120° \           ,\ α=60°$$ Czyli: $$|\sphericalangle ABC|=60° \           ,\ |\sphericalangle ACB|=60°$$ Krok 3. Zakończenie dowodzenia. Z naszej analizy wynika, że wszystkie kąty trójkąta \(ABC\) mają miarę \(60°\). Jest to charakterystyczna cecha trójkąta równobocznego, zatem udowadniając miary tych poszczególnych kątów możemy stwierdzić, że trójkąt \(ABC\) jest jak najbardziej trójkątem równobocznym.

Teoria:      
W trakcie opracowania