Na rysunku przedstawiono walec, stożek i kulę oraz niektóre ich wymiary.





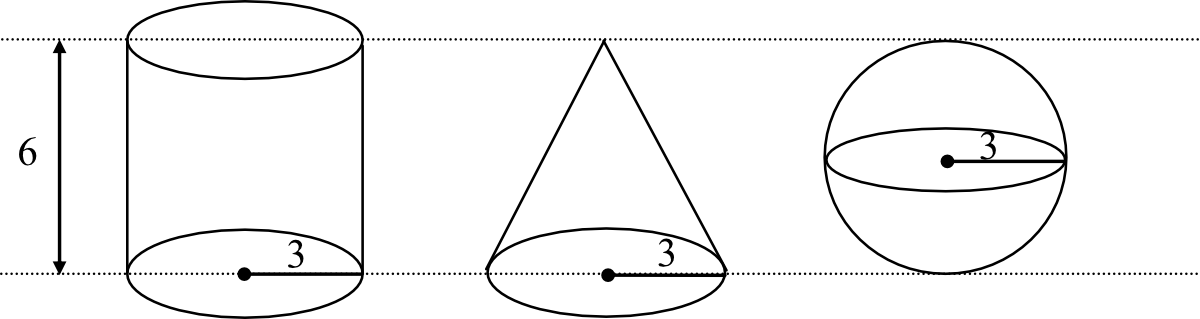
Na podstawie informacji przedstawionych na rysunku wybierz zdanie prawdziwe.

A Objętość kuli jest większa od objętości walca
B Objętość stożka jest większa od objętości kuli
C Objętość walca jest \(2\) razy większa od objętości kuli
D Objętość stożka jest \(3\) razy mniejsza od objętości walca

Odpowiedź:      

D

Rozwiązanie:      
To zadanie wymaga od nas nie tyle obliczeń każdej z objętości co przede wszystkim spostrzegawczości. Znając wzory na objętość walca i stożka wiemy doskonale, że różnią się tylko tym, że we wzorze na objętość stożka stoi dodatkowo mnożenie przez \(\frac{1}{3}\): $$V_{walca}=πr^2\cdot H \           ,\ V_{stożka}=\frac{1}{3}πr^2\cdot H$$ Skoro wszystkie wymiary brył są jednakowe, to na pewno objętość stożka będzie \(3\) razy mniejsza od objętości walca (właśnie przez to mnożenie przez \(\frac{1}{3}\)). To oznacza, że nawet bez dokonywania obliczeń możemy wybrać czwartą odpowiedź jako tą prawdziwą. Jeżeli jednak nie dostrzegamy takich zależności, to nic nie stoi na przeszkodzie by obliczyć objętości tych trzech brył: Krok 1. Obliczenie objętości walca. $$V_{w}=πr^2\cdot H \           ,\ V_{w}=π3^2\cdot6 \           ,\ V_{w}=π9\cdot6 \           ,\ V_{w}=54π$$ Krok 2. Obliczenie objętości stożka. $$V_{s}=\frac{1}{3}πr^2\cdot H \           ,\ V_{s}=\frac{1}{3}π\cdot9\cdot6 \           ,\ V_{s}=18π$$ Krok 3. Obliczenie objętości kuli. $$V_{k}=\frac{4}{3}πr^3 \           ,\ V_{k}=\frac{4}{3}π\cdot3^3 \           ,\ V_{k}=\frac{4}{3}π\cdot27 \           ,\ V_{k}=36π$$ Krok 4. Wybór właściwej odpowiedzi. Przyglądając się wynikom i odpowiedziom z treści zadania widzimy wyraźnie, że jedynym prawdziwym stwierdzeniem jest to zawarte w czwartej odpowiedzi, bo faktycznie objętość stożka jest \(3\) razy mniejsza od objętości walca.

Teoria:      
W trakcie opracowania