Na rysunku przedstawiono czworokąt zbudowany z dwóch trójkątów prostokątnych. Dane są długości boków \(|AB|=|BC|=1\) oraz \(|AD|=\sqrt{2}\).





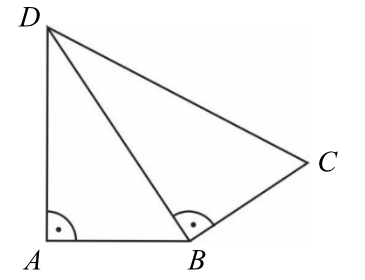
Długość boku \(CD\) jest równa:

A \(\sqrt{3}\)
B \(2\)
C \(3\)
D \(2\sqrt{2}\)

Odpowiedź:      

B

Rozwiązanie:      
Krok 1. Obliczenie długości boku \(BD\). Korzystając z Twierdzenia Pitagorasa otrzymamy: $$1^2+(\sqrt{2})^2=|BD|^2 \           ,\ 1+2=|BD|^2 \           ,\ |BD|^2=3 \           ,\ |BD|=\sqrt{3}$$ Krok 2. Obliczenie długości boku \(CD\). Z rysunku wynika, że trójkąt \(BCD\) jest trójkątem prostokątnym w którym znamy długości dwóch boków: \(|BC|=1\) oraz \(|BD|=\sqrt{3}\). Korzystając z Twierdzenia Pitagorasa możemy teraz obliczyć długość poszukiwanego boku \(CD\): $$1^2+(\sqrt{3})^2=|CD|^2 \           ,\ 1+3=|CD|^2 \           ,\ |CD|^2=4 \           ,\ |CD|=2$$

Teoria:      
W trakcie opracowania