Na rysunku przedstawiono równoległobok \(ABCD\) i trójkąt równoramienny \(AED\), w którym \(DE=AE\) . Miara kąta \(BCE\) jest równa \(106°\).





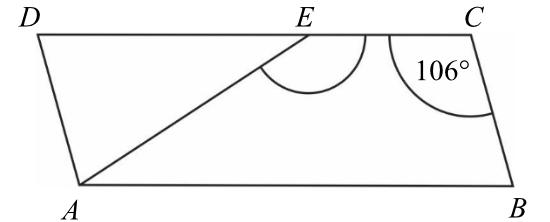
Jaką miarę ma kąt \(AEC\)?

A \(148°\)
B \(122°\)
C \(74°\)
D \(58°\)

Odpowiedź:      

A

Rozwiązanie:      
Krok 1. Obliczenie miary kąta \(ABC\). W równoległoboku kąty przy jednym ramieniu mają łączną miarę \(180°\). Skoro tak, to kąt \(ABC\) ma miarę: $$180°-106°=74°$$ Krok 2. Obliczenie miary kąta \(AED\). Skoro kąt \(ABC\) ma miarę \(74°\), to kąt \(ADE\) ma także miarę \(74°\). Wiemy, że trójkąt \(ADE\) jest równoramienny, zatem kąty przy jego podstawie muszą mieć tą samą miarę. Skoro tak, to kąt \(DAE\) jest również kątem o mierze \(74°\). Powstała nam więc następująca sytuacja: Teraz spójrzmy na trójkąt \(ADE\). Znamy miary dwóch kątów w tym trójkącie, zatem bez przeszkód obliczymy miarę tego trzeciego kąta: $$|\sphericalangle AED|=180°-74°-74°=32°$$ Krok 3. Obliczenie miary kąta \(AEC\). Kąty \(AED\) oraz \(AEC\) to kąty przyległe, a więc ich łączna miara wynosi \(180°\). Znając miarę kąta \(AED\) możemy zapisać, że: $$|\sphericalangle AEC|=180°-32°=148°$$

Teoria:      
W trakcie opracowania