Wskaż nierówność, która opisuje zaznaczony na osi liczbowej przedział otwarty \((-4, 2)\).

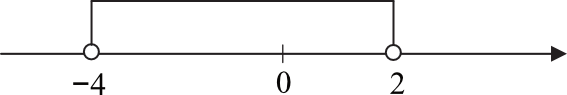
A \(|x-1|\lt3\)
B \(|x+3|\lt1\)
C \(|x+1|\lt3\)
D \(|x-3|\lt1\)

Odpowiedź:      

C

Rozwiązanie:      
Możemy rozwiązać każdą nierówność oddzielnie i sprawdzić które z rozwiązań będzie identyczne jak na rysunku, ale możemy też rozwiązać to nieco bardziej matematycznie. Po lewej stronie nierówności będziemy mieć zawsze \(|x-a|\), gdzie \(a\) jest punktem leżącym idealnie po środku między krańcami przedziałów (w naszym przypadku między \(-4\) oraz \(2\)). To oznacza, że: $$a=\frac{-4+2}{2}=\frac{-2}{2}=-1$$ Po lewej stronie nierówności będziemy mieć zatem \(|x-(-1)|\), czyli \(|x+1|\). I już w tym momencie moglibyśmy zakończyć rozwiązywanie, bo taka sytuacja pojawia się jedynie w trzeciej odpowiedzi. Gdybyśmy chcieli jeszcze mimo wszystko ustalić znak nierówności i liczbę po prawej stronie, to musimy spojrzeć na to jak dużo jednostek dzieli nasz punkt środkowy \(a=-1\) od punktów krańcowych. Między punktem środkowym \(a=-1\) oraz punktami krańcowymi \(-4\) oraz \(2\) mamy dokładnie po \(3\) jednostki w lewo i w prawo. Nas interesują wszystkie te wartości, które są oddalone od punktu środkowego o mniej niż \(3\) jednostki (tak aby zmieściły się w przedziale), stąd też ostatecznym rozwiązaniem będzie: $$|x+1|\lt3$$

Teoria:      
W trakcie opracowania