W pierścieniu kołowym cięciwa zewnętrznego okręgu ma długość \(10\) i jest styczna do wewnętrznego okręgu (zobacz rysunek).







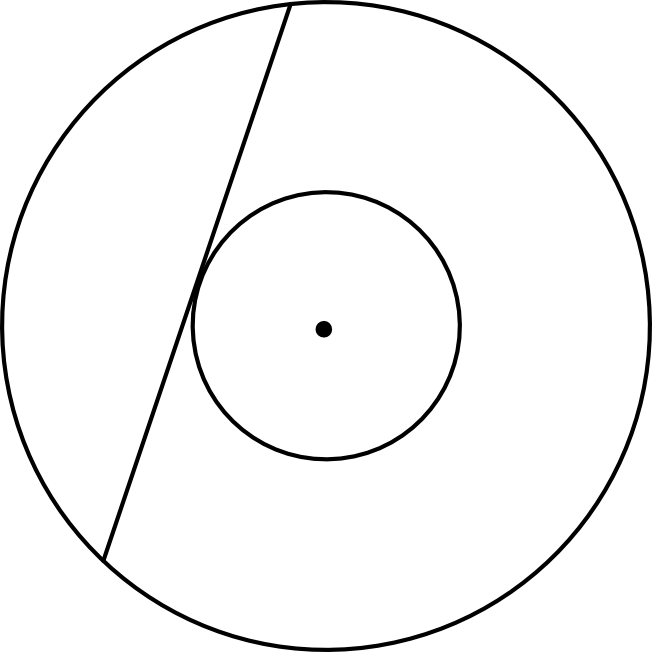
Wykaż, że pole tego pierścienia można wyrazić wzorem, w którym nie występują promienie wyznaczających go okręgów.

Odpowiedź:      

Udowodniono wykorzystując Twierdzenie Pitagorasa.

Rozwiązanie:      
Krok 1. Zapisanie wzoru na pole pierścienia. Pole pierścienia możemy zapisać jako różnicę między polem powierzchni dużego koła (o promieniu duże \(R\)) i małego (o promieniu małe \(r\)), zatem: $$P=πR^2-πr^2=π(R^2-r^2)$$ No i teraz naszym zadaniem jest doprowadzenie do sytuacji w której pozbędziemy się wartości promieni. Krok 2. Sporządzenie rysunku poglądowego. Wiedząc, że styczna jest zawsze prostopadła do promienia okręgu, możemy stworzyć następujący trójkąt prostokątny: Krok 3. Wyznaczenie wartości wyrażenia \(R^2-r^2\) z Twierdzenia Pitagorasa. Podstawiając do Twierdzenia Pitagorasa dane i oznaczenia z naszego rysunku otrzymamy: $$r^2+5^2=R^2 \           ,\ r^2+25=R^2 \           ,\ 25=R^2-r^2$$ Krok 4. Zakończenie dowodzenia. Podstawiając wartość \(R^2-r^2\) do wzoru na pole pierścienia otrzymamy, że: $$P=π(R^2-r^2) \           ,\ P=25π$$ I taki zapis kończy nasze dowodzenie, bo udało nam się określić wzór na pole pierścienia bez występowania długości promieni.

Teoria:      
W trakcie opracowania