Kwadrat \(K_{1}\) ma bok długości \(a\). Obok niego rysujemy kolejno kwadraty \(K_{2}, K_{3}, K_{4},...\) takie, że kolejny kwadrat ma bok połowę mniejszy od boku poprzedniego kwadratu (zobacz rysunek).







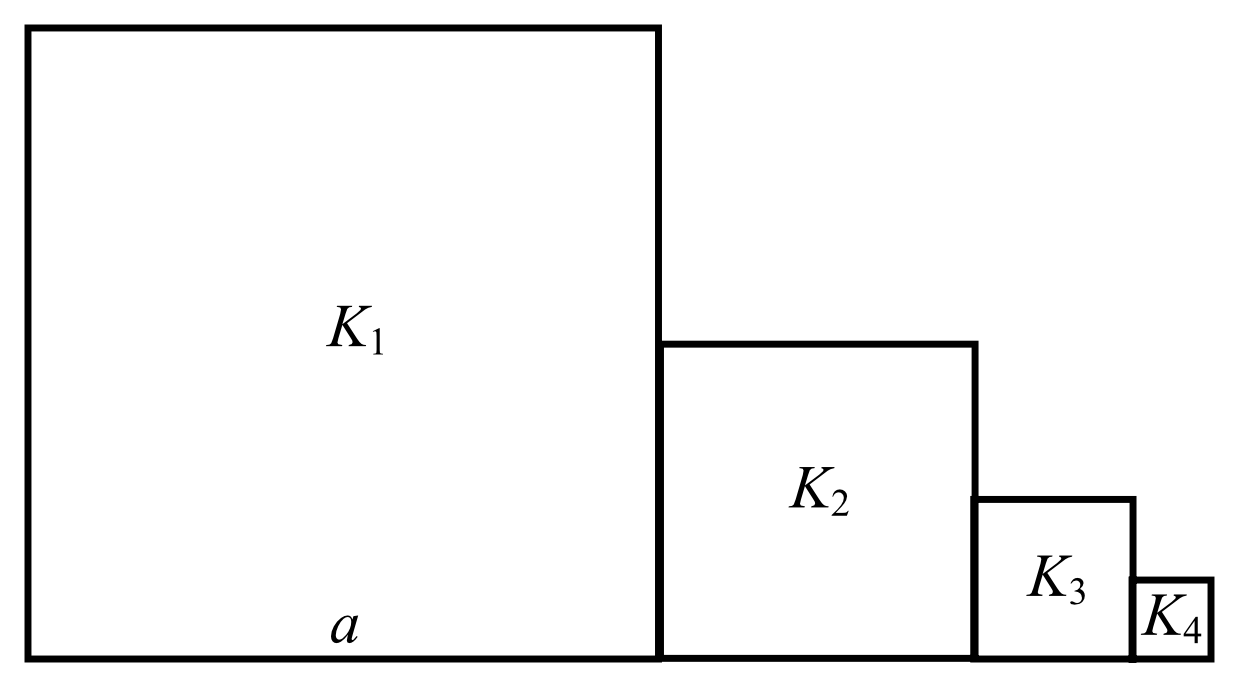
Wyznacz pole kwadratu \(K_{12}\).

Odpowiedź:      

\(P=\frac{a^2}{2^{22}}\)

Rozwiązanie:      
Krok 1. Wyznaczenie długości boku kwadratu \(K_{12}\). Pierwszy kwadrat ma długość boku równą \(a\). Drugi kwadrat ma długość boku równą \(\frac{a}{2}\). Trzeci kwadrat ma długość boku równą \(\frac{a}{2^2}\). Czwarty kwadrat ma długość boku równą \(\frac{a}{2^3}\). ... Dwunasty kwadrat ma długość boku równą \(\frac{a}{2^{11}}\). Krok 2. Obliczenie pola kwadratu \(K_{12}\). Podstawiając do wzoru na pole kwadratu długość boku równą \(\frac{a}{2^{11}}\) otrzymamy: $$P=\left(\frac{a}{2^{11}}\right)^2=\frac{a^2}{2^{22}}$$

Teoria:      
W trakcie opracowania