Trapez jest prostokątny. Trójkąty podobne \(ABD\) i \(CBD\) są równoramienne.





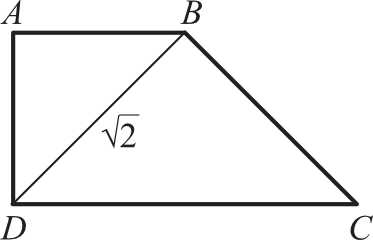
Obwód trapezu jest równy:

A \(4+2\sqrt{2}\)
B \(2\sqrt{2}\)
C \(4+\sqrt{2}\)
D \(4\)

Odpowiedź:      

C

Rozwiązanie:      
Z treści zadania można wyciągnąć informację, że obydwa trójkąty są równoramienne, a w zasadzie to muszą być i równoramienne i prostokątne, bo trapez jest prostokątny więc \(|\sphericalangle DAB|=90°\). Dzięki tej obserwacji będziemy mogli poobliczać długości poszczególnych boków stosując albo własności trójkątów o kątach \(45°, 45°, 90°\) (bo takie kąty występują zawsze w trójkątach prostokątnych równoramiennych), albo stosując Twierdzenie Pitagorasa, albo wykorzystując własności trójkątów podobnych. Krok 1. Obliczenie długości boków \(BC\) oraz \(CD\). Jeżeli trójkąt \(CBD\) jest równoramienny to znaczy, że \(|BD|=|BC|=\sqrt{2}\). W ten oto sposób jesteśmy w stanie obliczyć także długość boku \(|DC|\) korzystając z Twierdzenia Pitagorasa: $$(\sqrt{2})^2+(\sqrt{2})^2=|DC|^2 \           ,\ 2+2=|DC|^2 \           ,\ |DC|^2=4 \           ,\ |DC|=2 \quad\lor\quad |DC|=-2$$ Wartość ujemną oczywiście odrzucamy, zatem \(|DC|=2\). Krok 2. Obliczenie długości boków \(AB\) oraz \(AD\). Spójrzmy na trójkąt \(ABD\). Odcinki \(AB\) oraz \(AD\) mają jednakową miarę. Także tutaj do ich obliczenia możemy zastosować własności trójkątów o kątach \(45°, 45°, 90°\) (wiedząc że przeciwprostokątna jest równa \(\sqrt{2}\) bez problemu możemy stwierdzić, że w takim razie przyprostokątne mają długość \(1\)), ale jeśli nie dostrzegliśmy że to jest akurat taki trójkąt o charakterystycznych kątach, to możemy ułożyć prostą proporcję, korzystając z informacji że są to trójkąty podobne: $$\frac{|DC|}{|DB|}=\frac{|DB|}{|AD|} \           ,\ \frac{2}{\sqrt{2}}=\frac{\sqrt{2}}{|AD|}$$ Mnożąc na krzyż otrzymamy $$2=2|AD| \           ,\ |AD|=1$$ Skoro odcinki \(AD\) oraz \(AB\) mają jednakową miarę, to możemy zapisać, że \(|AD|=1\) oraz \(|AB|=1\). Krok 3. Obliczenie obwodu trapezu. Znamy już wszystkie długości boków, zatem: $$Obw=2+\sqrt{2}+1+1=4+\sqrt{2}$$

Teoria:      
W trakcie opracowania