Punkty \(G\) i \(H\) są środkami okręgów. Punkt \(E\) leży na okręgu o środku w punkcie \(G\), punkt \(F\) leży na okręgu o środku w punkcie \(H\) oraz \(|GH|=3\) i \(|EF|=8\) (patrz rysunek).





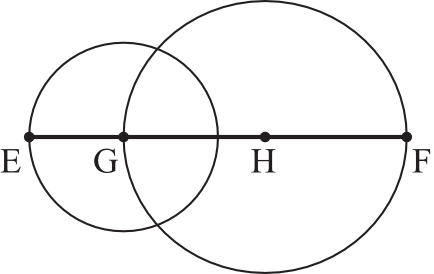
Wtedy pole koła ograniczonego okręgiem o środku w punkcie \(H\) jest większe od pola koła ograniczonego okręgiem o środku w punkcie \(G\) o:

A \(25π\)
B \(9π\)
C \(14π\)
D \(5π\)

Odpowiedź:      

D

Rozwiązanie:      
Krok 1. Obliczenie długości promienia \(EG\). Odcinek \(EF\) składa się z sumy odcinków \(|EG|\), \(|GH|\) oraz \(|HF|\). Z rysunku wynika, że |\(EG|=r\) oraz \(|GH|=|HF|=3\), zatem możemy ułożyć następujące równanie: $$|EG|+|GH|+|HF|=8 \           ,\ |EG|+3+3=8 \           ,\ |EG|+6=8 \           ,\ |EG|=2$$ Krok 2. Obliczenie pola powierzchni dużego koła. Długość promienia dużego koła jest podana w treści zadania i jest równa \(|GH|=3\), zatem: $$P_{d}=πr^2 \           ,\ P_{d}=π\cdot3^2 \           ,\ P_{d}=9π$$ Krok 3. Obliczenie pola powierzchni małego koła. Promień małego koła obliczyliśmy w pierwszym kroku, zatem: $$P_{m}=πr^2 \           ,\ P_{m}=π\cdot2^2 \           ,\ P_{m}=4π$$ Krok 4. Obliczenie różnicy pól powierzchni. Na koniec musimy zgodnie z poleceniem obliczyć różnicę pól powierzchni: $$P_{d}-P_{m}=9π-4π=5π$$

Teoria:      
W trakcie opracowania